题目内容
某生物实验室需培育一群有益菌.现有60个活体样本,经过两轮培植后,总和达24000个,其中每个有益菌每一次可分裂出若干个相同数目的有益菌.
(1)每轮分裂中平均每个有益菌可分裂出多少个有益菌?
(2)按照这样的分裂速度,经过三轮培植后有多少个有益菌?
【考点】一元二次方程的应用.
【分析】(1)设每轮分裂中平均每个有益菌可分裂出x个有益菌,则第一轮分裂后有(60+60x)个,第二轮分裂出(60+60x)x,两次加起来共有24000建立方程求出其解就可以;
(2)根据(1)的结论,就可以得出第三轮共有60(1+x)3个有益菌,将x的值代入就可以得出结论.
【解答】解:(1)设每轮分裂中平均每个有益菌可分裂出x个有益菌,由题意,得
60(1+x)+60x(1+x)=24000,
60(1+x)(1+x)=24000,
解得:x1=19,x2=﹣21(舍去),
∴x=19.
答:每轮分裂中平均每个有益菌可分裂出19个有益菌.
(2)由题意,得
60×(1+19)3=480000个.
答:经过三轮培植后有480000个有益菌.
【点评】本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时分别表示出每轮分解后的总数是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的值为( )
的值为( ) D.
D.
 ,BD=
,BD= ,则AB的长为( )
,则AB的长为( )
 的对称轴、顶点坐标和最值.
的对称轴、顶点坐标和最值.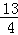 ,y1),B(
,y1),B(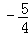 ,y2),C(
,y2),C(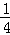 ,y3)为二次函数y=x2+4x﹣5的图象上的三点,则y1,y2,y3的大小关系是( )
,y3)为二次函数y=x2+4x﹣5的图象上的三点,则y1,y2,y3的大小关系是( ) 如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
 B.
B. C.
C. D.
D.
