题目内容
18．
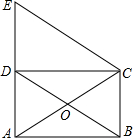如图，矩形ABCD的对角线AC、BD相交于点O，过点C作BD的平行线与AD的延长线相交于点E．求证：△ACE是等腰三角形．
分析 根据矩形的性质求出AC=BD，AD∥BC，根据平行四边形的判定推出四边形DECB是平行四边形，根据平行四边形的性质得出BD=CE即可．
解答 证明：∵四边形ABCD是矩形，
∴AC=BD，AD∥BC，
即DE∥BC，
∵BD∥CE，
∴四边形DECB是平行四边形，
∴BD=CE，
∴AC=CE，
∴△ACE是等腰三角形．
点评 本题考查了矩形的性质，平行四边形的判定和性质，等腰三角形的判定的应用，解此题的关键是求出AC=BD和得出四边形DECB是平行四边形，注意：矩形的对角线相等，矩形的对边平行．
练习册系列答案
相关题目
如图，OP=1，过P作PP1⊥OP且PP1=1，得OP1=$\sqrt{2}$；再过P1作P1P2⊥OP1且P1P2=1，得OP2=$\sqrt{3}$；又过P2作P2P3⊥OP2且P2P3=1，得OP3=2…依此法继续作下去，得${S_{△O{P_{2014}}{P_{2015}}}}$=$\frac{\sqrt{2015}}{2}$．
如图，?ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点．若AC+BD=24厘米，△OAB的周长是18厘米，则EF=3厘米．
13．下列各式不是一元一次不等式组的是（ ）
| A． | $\left\{\begin{array}{l}{x＞3}\\{x＜1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{3x＜5}\\{2x-1＜9}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x-1＞3}\\{y+2＜0}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x-1＞3}\\{x-3＜2}\\{2x-1＜5}\end{array}\right.$ |
如图，点P在平行四边形ABCD内，且∠ABP=∠ADP，求证：∠DAP=∠DCP．
如图，在?ABCD中，AE，BF，CM，DN分别是∠DAB，∠ABC，∠BCD，∠CDA的角平分线．求证：四边形GHKL是矩形．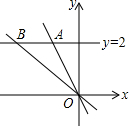
如图，直线y=2分别交正比例函数y=-2x，y=-$\frac{1}{2}$x的图象于A，B两点，求S△AOB．