题目内容
16.已知$\frac{2a-b}{a+b}$=$\frac{1}{3}$,则$\frac{a}{b}$=$\frac{4}{5}$.分析 利用内项之积等于外项之积得到6a-3b=a+b,整理得到5a=4b,然后再根据比例性质即可得到$\frac{a}{b}$的值.
解答 解:∵$\frac{2a-b}{a+b}$=$\frac{1}{3}$,
∴6a-3b=a+b,
∴5a=4b,
∴$\frac{a}{b}$=$\frac{4}{5}$.
故答案为$\frac{4}{5}$.
点评 本题考查了比例的性质:常用的性质有:内项之积等于外项之积;合比性质;分比性质;合分比性;等比性质.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
4.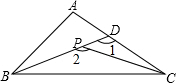 如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
 如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )| A. | ∠2>∠A>∠1 | B. | ∠2>∠1>∠A | C. | ∠1>∠A>∠2 | D. | ∠A>∠1>∠2 |
5. 实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
 实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )| A. | x+y+z>0 | B. | x+y+z<0 | C. | xy<yz | D. | xy<xz |

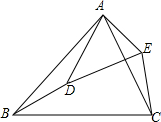 已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.
已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.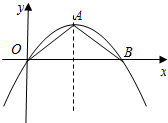 如图,已知抛物线y=-$\frac{1}{4}$x2+x的顶点为A,经过原点O,与x轴的另一个交点为B.在抛物线上求点M,使△AOB的面积是△MOB面积的2倍.
如图,已知抛物线y=-$\frac{1}{4}$x2+x的顶点为A,经过原点O,与x轴的另一个交点为B.在抛物线上求点M,使△AOB的面积是△MOB面积的2倍.