题目内容
观察下列各式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
…
(1)(x-1)(x10+x9+x8+…+x+1)= ;
(2)试求:1+2+22+23+…+263的值;
(3)判断22010+22009+22008+…+22+2+1的值的末位数字.(要有适当的过程)
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
…
(1)(x-1)(x10+x9+x8+…+x+1)=
(2)试求:1+2+22+23+…+263的值;
(3)判断22010+22009+22008+…+22+2+1的值的末位数字.(要有适当的过程)
考点:整式的混合运算,尾数特征
专题:规律型
分析:(1)根据已知式子的特点得出即可;
(2)先乘以2-1,符合已知式子的特点,再得出答案即可;
(3)先乘以2-1,求出式子的结果,再求出22011的个位数字,最后即可得出答案.
(2)先乘以2-1,符合已知式子的特点,再得出答案即可;
(3)先乘以2-1,求出式子的结果,再求出22011的个位数字,最后即可得出答案.
解答:解:(1)(x-1)(x10+x9+x8+…+x+1)=x11-1,
故答案为:x11-1;
(2)1+2+22+23+…+263的
=(2-1)×(263+262+…+23+22+2+1)
=264-1;
(3)22010+22009+22008+…+22+2+1的值
=(2-1)×(22010+22009+22008+…+22+2+1)
=22011-1,
∵21=2,22=4,23=8,24=16,25=32,26=64,…,
2011÷4=502…3,
∴22011的个位数字是8,
∴22010+22009+22008+…+22+2+1的值的末位数字是7.
故答案为:x11-1;
(2)1+2+22+23+…+263的
=(2-1)×(263+262+…+23+22+2+1)
=264-1;
(3)22010+22009+22008+…+22+2+1的值
=(2-1)×(22010+22009+22008+…+22+2+1)
=22011-1,
∵21=2,22=4,23=8,24=16,25=32,26=64,…,
2011÷4=502…3,
∴22011的个位数字是8,
∴22010+22009+22008+…+22+2+1的值的末位数字是7.
点评:本题考查了整式的混合运算和求值的应用,主要考查学生阅读理解能力,题目比较好,但是有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
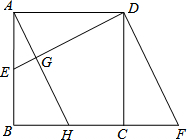 如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE. 画y=2x+1的图象.
画y=2x+1的图象.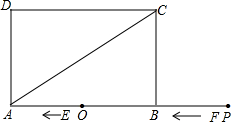 如图,矩形ABCD中,AB=6,BC=2
如图,矩形ABCD中,AB=6,BC=2