题目内容
已知x、y为正数,且|x2-4|+(y2-16)2=0,如果以x、y的长为直角边作一个直角三角形,那么这个直角三角形的斜边长为 .
考点:勾股定理,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:根据非负数的性质列式求出x2、y2,再利用勾股定理列式计算即可得解.
解答:解:由题意得,x2-4=0,y2-16=0,
所以,x2=4,y2=16,
由勾股定理得,斜边的平方=x2+y2=4+16=20,
所以,斜边=
=2
.
故答案为:2
.
所以,x2=4,y2=16,
由勾股定理得,斜边的平方=x2+y2=4+16=20,
所以,斜边=
| 20 |
| 5 |
故答案为:2
| 5 |
点评:本题考查了勾股定理,非负数的性质,几个非负数的和为0时,这几个非负数都为0列出方程是解题的关键.

练习册系列答案
相关题目
 下列图形中,既是轴对称图形又是中心对称图形的共有( )个.
下列图形中,既是轴对称图形又是中心对称图形的共有( )个.| A、1 | B、2 | C、3 | D、4 |
相反数是它本身的数是( )
| A、1 | B、-1 | C、0 | D、不存在 |
用科学记数法表示的数1.001×105的整数位数有( )
| A、3位 | B、4位 | C、5位 | D、6位 |
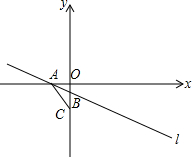 如图,已知直线l:y=-
如图,已知直线l:y=-