题目内容
 如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,
如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,(1)求EF的长.
(2)若点E以1个单位/秒的速度从点B向点A匀速运动,到点A停止运动,运动时间为t,其他条件不变,设在此运动过程中,由点A、E、F、C、D为顶点构成图形面积为S,求S与t的关系表达式.
考点:梯形
专题:
分析:(1)可过点D作DG⊥BC于点G,解直角三角形DGC,求出DG=AB的长,进一步求出BE,再解直角三角形BEF,再解这个三角形即可;
(2)过点A作AH∥CD交BC于点H,根据S=S△ABH-S△BEF+S平行四边形AHCD即可得出结论.
(2)过点A作AH∥CD交BC于点H,根据S=S△ABH-S△BEF+S平行四边形AHCD即可得出结论.
解答: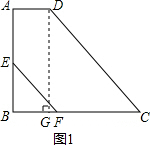 解:(1)如图1,过点D作DG⊥BC于点G.
解:(1)如图1,过点D作DG⊥BC于点G.
∵AD∥BC,∠B=90°,
∴∠A=90°.
∴四边形ABGD为矩形.
∴BG=AD=1,AB=DG.
∵BC=4,
∴GC=3.
∵∠DGC=90°,∠C=45°,
∴∠CDG=45°.
∴DG=GC=3.
∴AB=3.
又∵E为AB中点,
∴BE=
AB=
.
∵EF∥DC,
∴∠EFB=45°.
在△BEF中,
∵∠B=90°.
∴EF=sin45°=
.
(2)如图2,过点A作AH∥CD交BC于点H,则S=S△ABH-S△BEF+S平行四边形AHCD,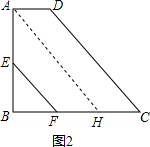
∵AD=1,AD∥BC,AH∥CD,
∴CH=AD=1.
∵由(1)知,AB=BH=3,BE=t,EF∥AH,
∴S=S△ABH-S△BEF+S平行四边形AHCD
=
×3×3-
t2+1×3
=
-
t2.
 解:(1)如图1,过点D作DG⊥BC于点G.
解:(1)如图1,过点D作DG⊥BC于点G.∵AD∥BC,∠B=90°,
∴∠A=90°.
∴四边形ABGD为矩形.
∴BG=AD=1,AB=DG.
∵BC=4,
∴GC=3.
∵∠DGC=90°,∠C=45°,
∴∠CDG=45°.
∴DG=GC=3.
∴AB=3.
又∵E为AB中点,
∴BE=
| 1 |
| 2 |
| 3 |
| 2 |
∵EF∥DC,
∴∠EFB=45°.
在△BEF中,
∵∠B=90°.
∴EF=sin45°=
| 3 |
| 2 |
| 2 |
(2)如图2,过点A作AH∥CD交BC于点H,则S=S△ABH-S△BEF+S平行四边形AHCD,

∵AD=1,AD∥BC,AH∥CD,
∴CH=AD=1.
∵由(1)知,AB=BH=3,BE=t,EF∥AH,
∴S=S△ABH-S△BEF+S平行四边形AHCD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 15 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是梯形,根据题意作出辅助线,构造出矩形及平行四边形是解答此题的关键.

练习册系列答案
相关题目
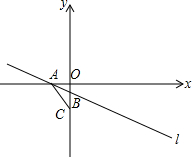 如图,已知直线l:y=-
如图,已知直线l:y=-
 如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,求∠A.
如图,BO、CO分别平分∠ABC、∠ACB,且∠BOC=110°,求∠A.