题目内容
从-1,1,2,4这四个数中,任取两个不同的数作为m、n的值,恰好使得关于x、y的二元一次方程组
的解都是负数,且点(m,n)恰好落在直线y=-x+3上的概率为 .
|
考点:列表法与树状图法,二元一次方程组的解,一次函数图象上点的坐标特征
专题:
分析:首先用列表法或树形图得到所用可能的情况,若使点(m,n)落在直线y=-x+3上,则x+y=3,由此得到m、n的关系式,再根据恰好使得关于x,y的二元一次方程组
的解都是负数,即可求出m,n的值,由此可得到使得关于x、y的二元一次方程组
的解都是负数,且点(m,n)落在直线y=-x+3上的概率.
|
|
解答:解:画树状图得:
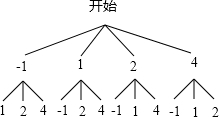
由上图可知,共有12种等可能的结果.
若使点(m,n)落在直线y=-x+3上,则x+y=3,
∴点(m,n)可以是(-1,4)、(1,2)、(2,1)、(4,-1),
∵恰好使得关于x,y的二元一次方程组
有负数解,
∴点(m,n)可以是(4,-1),
∴使得关于x、y的二元一次方程组
的解都是负数,且点(m,n)恰好落在直线y=-x+3上的概率为
.
故答案为:
.

由上图可知,共有12种等可能的结果.
若使点(m,n)落在直线y=-x+3上,则x+y=3,
∴点(m,n)可以是(-1,4)、(1,2)、(2,1)、(4,-1),
∵恰好使得关于x,y的二元一次方程组
|
∴点(m,n)可以是(4,-1),
∴使得关于x、y的二元一次方程组
|
| 1 |
| 12 |
故答案为:
| 1 |
| 12 |
点评:此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
相反数是它本身的数是( )
| A、1 | B、-1 | C、0 | D、不存在 |
用科学记数法表示的数1.001×105的整数位数有( )
| A、3位 | B、4位 | C、5位 | D、6位 |
 如图,函数y=-(x-h)2+k的图象,则其解析式为
如图,函数y=-(x-h)2+k的图象,则其解析式为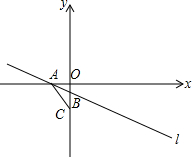 如图,已知直线l:y=-
如图,已知直线l:y=- 如图,边长为2正方形ABCD中,BD为对角线,AE∥BD,且DE=DB,DE与AB交于F点,则EF=
如图,边长为2正方形ABCD中,BD为对角线,AE∥BD,且DE=DB,DE与AB交于F点,则EF=
 已知△ABC和△ADE中,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,M为中点,连接DM,BM.求证:
已知△ABC和△ADE中,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,M为中点,连接DM,BM.求证: