题目内容
 在△ABC中,∠ABC的角平分线交AC边于点D.
在△ABC中,∠ABC的角平分线交AC边于点D.(1)用尺规作∠ABC的角平分线BD(不写作法,保留作图痕迹)
(2)若BD=9,sin∠DBC=
| 1 |
| 3 |
| 2 |
考点:作图—基本作图,解直角三角形
专题:
分析:(1)①以点B为圆心,以任意长为半径画弧,两弧交角ABC两边于点M,N;
②分别以点M,N为圆心,以大于
MN的长度为半径画弧,两弧交于点E;
③作射线BE交AC与D.
则线段BD为△ABC的角平分线.
(2)过点D作DE⊥BC,垂足为点E,首先求得DE,然后利用勾股定理求得BE,从而根据BC的长求得EC,然后利用正切的定义求得答案即可.
②分别以点M,N为圆心,以大于
| 1 |
| 2 |
③作射线BE交AC与D.
则线段BD为△ABC的角平分线.
(2)过点D作DE⊥BC,垂足为点E,首先求得DE,然后利用勾股定理求得BE,从而根据BC的长求得EC,然后利用正切的定义求得答案即可.
解答:解:(1)如图:

(2)过点D作DE⊥BC,垂足为点E,

∵在Rt△BDE中,BD=9,sin∠DBC=
,
∴DE=3,
∴BE=
=6
,
∵BC=7
,
∴EC=
,
∴在Rt△DEC中,
∴tanC=
=
=
.

(2)过点D作DE⊥BC,垂足为点E,

∵在Rt△BDE中,BD=9,sin∠DBC=
| 1 |
| 3 |
∴DE=3,
∴BE=
| BD2-DE2 |
| 2 |
∵BC=7
| 2 |
∴EC=
| 2 |
∴在Rt△DEC中,
∴tanC=
| DE |
| EC |
| 3 | ||
|
| 3 |
| 2 |
| 2 |
点评:本题主要考查基本作图:作一个角的平分线,牢记一些基本作图是解答本题的关键.

练习册系列答案
相关题目

 在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.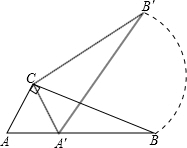 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )