题目内容
为倡导“低碳生活”,人们常选择以自行车作为代步工具、图(1)所示的是一辆自行车的实物图.图(2)是这辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45cm和60cm,且它们互相垂直,座杆CE的长为20cm.点A、C、E在同一条直线上,且∠CAB=75°.(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732)

(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm).

(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm).
考点:解直角三角形的应用
专题:几何图形问题,转化思想
分析:(1)在Rt△ACD中利用勾股定理求AD即可.
(2)过点E作EF⊥AB,在RT△EFA中,利用三角函数求EF=AEsin75°,即可得到答案.
(2)过点E作EF⊥AB,在RT△EFA中,利用三角函数求EF=AEsin75°,即可得到答案.
解答: 解:(1)∵在Rt△ACD中,AC=45cm,DC=60cm
解:(1)∵在Rt△ACD中,AC=45cm,DC=60cm
∴AD=
=75(cm),
∴车架档AD的长是75cm;
(2)过点E作EF⊥AB,垂足为F,
∵AE=AC+CE=(45+20)cm,
∴EF=AEsin75°=(45+20)sin75°≈62.7835≈63(cm),
∴车座点E到车架档AB的距离约是63cm.
 解:(1)∵在Rt△ACD中,AC=45cm,DC=60cm
解:(1)∵在Rt△ACD中,AC=45cm,DC=60cm∴AD=
| 452+602 |
∴车架档AD的长是75cm;
(2)过点E作EF⊥AB,垂足为F,
∵AE=AC+CE=(45+20)cm,
∴EF=AEsin75°=(45+20)sin75°≈62.7835≈63(cm),
∴车座点E到车架档AB的距离约是63cm.
点评:此题主要考查了勾股定理与三角函数的应用,关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
下列实数中是无理数的是( )
A、
| ||||
| B、2-2 | ||||
C、5.
| ||||
| D、sin45° |
 如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.过点B的直线y=-
如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.过点B的直线y=- (1)已知反比例函数y=
(1)已知反比例函数y=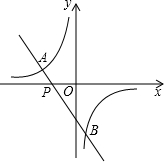 如图,一次函数y=kx+b(k≠0)的图象过点P(-
如图,一次函数y=kx+b(k≠0)的图象过点P(- 在△ABC中,∠ABC的角平分线交AC边于点D.
在△ABC中,∠ABC的角平分线交AC边于点D.