题目内容
4. 已知:如图,在△ODC中,∠D=90°,CE是∠DCO的角平分线,且OE⊥CE,过点E作EF⊥OC于点F,猜想:线段EF与OD之间的数量关系,并证明.
已知:如图,在△ODC中,∠D=90°,CE是∠DCO的角平分线,且OE⊥CE,过点E作EF⊥OC于点F,猜想:线段EF与OD之间的数量关系,并证明.
分析 延长CD和OE,使CD、OE相交于H,过E点作EG⊥HD,根据△OCE≌△HCE可得OE=EH,再判断出EG是△OHD的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半可得EG=$\frac{1}{2}$OD,然后根据角平分线上的点到角的两边距离相等可得EF=EG,等量代换即可得证.
解答 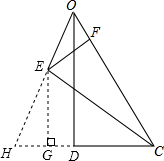 解:如图,延长CD和OE,交于H,过E点作EG⊥HD,
解:如图,延长CD和OE,交于H,过E点作EG⊥HD,
∵EC是∠DCO的平分线,且EC⊥OE,
∴由∠CEO=∠CEH=90°,CE=CE,∠OCE=∠HCE可得,△OCE≌△HCE,
∴OE=EH,
∵EG⊥HD,OD⊥HD,
∴EG∥OD,
∴EG是△OHD的中位线,
∴EG=$\frac{1}{2}$OD,
又∵EC是∠DCO的平分线,EG⊥HD,EF⊥OC,
∴EG=EF,
∴EF=$\frac{1}{2}$OD.
点评 本题主要考查了角平分线的性质以及三角形中位线定理,解决问题的关键是作辅助线,构造全等三角形和三角形的中位线.解题时注意:角的平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目
12. 如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )
如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )
 如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )
如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )| A. | 105° | B. | 115° | C. | 125° | D. | 135° |
13.某乡镇企业生产部有技术工人15人,为了合理制定产品的每月定额,统计了15人月的加工零件个数:
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如负责人把每位工人的月加工零件数定为260(件),你认为这个定额是否合理,为什么?
| 每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
| 人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(2)假如负责人把每位工人的月加工零件数定为260(件),你认为这个定额是否合理,为什么?
13.体积为80的正方体的棱长在( )
| A. | 3到4之间 | B. | 4到5之间 | C. | 5到6之间 | D. | 6到7之间 |
 在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,过点E作EF∥BC,与AC交于点F.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,过点E作EF∥BC,与AC交于点F.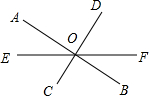 如图,直线AB与CD相交于点O,若∠AOD=70°,∠BOE-∠BOC=50°,求∠DOE的度数.
如图,直线AB与CD相交于点O,若∠AOD=70°,∠BOE-∠BOC=50°,求∠DOE的度数.