题目内容
15.根据题意列出方程组(1)甲、乙两人在一环形场地上从点A同时同向匀速跑步,甲的速度是乙的速度的2.5倍,4min后两人首次相遇,此时乙还需要跑300m跑完第一圈.求甲、乙两人的速度及环形场地的周长.
(2)将若干只鸡放人若干笼中,若每个笼中放4只.则有一鸡无笼可放;若每个笼里放5只.则有一笼无鸡可放,问有多少只鸡,多少个笼?
分析 (1)设乙的速度为x米/分,则甲的速度为2.5x米/分,环形场地的周长为y米,根据环形问题的数量关系,同时、同地、同向而行首次相遇快者走的路程-慢者走的路程=环形周长建立方程即可;
(2)由题意可知鸡与笼的总数是不变的,由此可得两个等量关系式:即每笼放4只时,笼中鸡的总数+1=鸡的总数;当笼中放5只鸡时,(笼的总数-1)×5=鸡的总数.
解答 解:(1)设乙的速度为x米/分,则甲的速度为2.5x米/分,环形场地的周长为y米,由题意,得
$\left\{\begin{array}{l}{2.5x×4-4x=y}\\{4x+300=y}\end{array}\right.$,
即$\left\{\begin{array}{l}{6x-y=0}\\{4x-y=-300}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=150}\\{y=900}\end{array}\right.$,
故2.5x=375(米/分),
答:甲、乙两人的速度分别为:375米/分,150米/分及环形场地的周长为900m.
(2)解:设笼的总数为x,鸡的总数为y只,根据题意可得:
则$\left\{\begin{array}{l}{4x+1=y}\\{5(x-1)=y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=6}\\{y=25}\end{array}\right.$,
答:笼的总数为6个,鸡的总数为25只.
点评 本题考查了列二元一次方程组解环形问题的运用,解答时运用环形问题的数量关系建立方程是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若(a-3)2+|b-4|=0,则(a-b)2004的值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2016 |
10. 如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
 如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )
如图是小明作线段AB的垂直平分线的作法及作图痕迹,则四边形ADBC一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 无法确定 |
3. 如图,AB∥CD,∠1=100°,∠2=120°,则∠α等于( )
如图,AB∥CD,∠1=100°,∠2=120°,则∠α等于( )
 如图,AB∥CD,∠1=100°,∠2=120°,则∠α等于( )
如图,AB∥CD,∠1=100°,∠2=120°,则∠α等于( )| A. | 100° | B. | 80° | C. | 60° | D. | 40° |

 如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.
如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.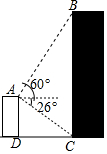 如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)