题目内容
16.把下列各数填入相应的集合内:$\sqrt{12}$,0,$\root{3}{-8}$.-$\frac{1}{6}$,0.2$\stackrel{•}{5}$,-$\frac{π}{3}$,0.3030030003…(相邻两个3之间0的个数逐次加1).
(1)正实数集合{$\sqrt{12}$,0,0.2$\stackrel{•}{5}$,0.3030030003……}
(2)负实数集合{$\root{3}{-8}$,-$\frac{1}{6}$,-$\frac{π}{3}$…}
(3)有理数集合{0,$\root{3}{-8}$.-$\frac{1}{6}$,0.2$\stackrel{•}{5}$…}
(4)无理数集合{$\sqrt{12}$,-$\frac{π}{3}$,0.3030030003……}.
分析 根据实数的分类填空.
解答 解:$\sqrt{12}$=2$\sqrt{3}$,$\root{3}{-8}$=-2,
(1)正实数集合{$\sqrt{12}$,0,0.2$\stackrel{•}{5}$,0.3030030003…}
(2)负实数集合{$\root{3}{-8}$,-$\frac{1}{6}$,-$\frac{π}{3}$}
(3)有理数集合{0,$\root{3}{-8}$.-$\frac{1}{6}$,0.2$\stackrel{•}{5}$}
(4)无理数集合{$\sqrt{12}$,-$\frac{π}{3}$,0.3030030003…}.
故答案是:$\sqrt{12}$,0,0.2$\stackrel{•}{5}$,0.3030030003…;$\root{3}{-8}$,-$\frac{1}{6}$,-$\frac{π}{3}$;0,$\root{3}{-8}$.-$\frac{1}{6}$,0.2$\stackrel{•}{5}$;$\sqrt{12}$,-$\frac{π}{3}$,0.3030030003….
点评 此题主要考查了实数、无理数、有理数之间的关系,有理数都可以化为小数,其中整数可以看作小数点后面是零的小数,分数都可以化为有限小数或无限循环小数;无理数是无限不循环小数,其中有开方开不尽的数.

练习册系列答案
相关题目
8.在锐角三角形中,最小的角不可能是( )
| A. | 60° | B. | 55° | C. | 45° | D. | 15° |
5.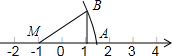 如图,MA=MB,则数轴上点A对应的数是( )
如图,MA=MB,则数轴上点A对应的数是( )
 如图,MA=MB,则数轴上点A对应的数是( )
如图,MA=MB,则数轴上点A对应的数是( )| A. | $\sqrt{5}$+1 | B. | -$\sqrt{5}$+1 | C. | -$\sqrt{5}$-1 | D. | $\sqrt{5}$-1 |
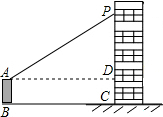 某消防队员进行消防演练,在模拟现场,有一建筑物发生了火灾,消防车到达后,发现最多只能靠近建筑物12米,即AD=BC=12米,此时建筑物中距离地面11.8米高的P处有一被困人员需要救援,已知消防云梯底部A距离地面2.8米,即AB=2.8米,则消防车的云梯至少要伸长15米.
某消防队员进行消防演练,在模拟现场,有一建筑物发生了火灾,消防车到达后,发现最多只能靠近建筑物12米,即AD=BC=12米,此时建筑物中距离地面11.8米高的P处有一被困人员需要救援,已知消防云梯底部A距离地面2.8米,即AB=2.8米,则消防车的云梯至少要伸长15米.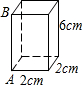 如图,长方体的底面是边长为2cm的正方形,高是6cm.
如图,长方体的底面是边长为2cm的正方形,高是6cm. 如图,y=-x2+(m-2)x+3(m+1),
如图,y=-x2+(m-2)x+3(m+1),