题目内容
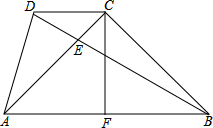 已知:如图,点C是等腰直角△ABC的直角顶点,DC∥AB,BD=AB,BD交AC于点E,CF⊥AB,垂足为F,求证:
已知:如图,点C是等腰直角△ABC的直角顶点,DC∥AB,BD=AB,BD交AC于点E,CF⊥AB,垂足为F,求证:(1)∠ABD=30°;
(2)AD=AE.
考点:等腰直角三角形,平行线之间的距离,等腰三角形的判定与性质,含30度角的直角三角形
专题:证明题
分析:(1)过D作DG垂直于AB,由AB与CD平行,利用平行线间的距离相等得到DG=CF,由CF垂直于AB,且三角形ABC为等腰直角三角形得到CF为斜边AB上的中线,得到AB=2CF,即DB=2DG,即可得证;
(2)由∠AED为三角形AEB外角,求出∠AED=75°,再由三角形ABD为顶角为30°的等腰三角形,求出∠ADE=75°,利用等角对等边即可得证.
(2)由∠AED为三角形AEB外角,求出∠AED=75°,再由三角形ABD为顶角为30°的等腰三角形,求出∠ADE=75°,利用等角对等边即可得证.
解答: 证明:(1)过D作DG⊥AB,交AB于点G,
证明:(1)过D作DG⊥AB,交AB于点G,
∵DC∥AB,
∴DG=CF,
∵△ABC为等腰直角三角形,且CF⊥AB,
∴CF为斜边AB上的中线,
∴CF=
AB,
∵AB=BD,
∴DG=
BD,
则在Rt△BDG中,∠ABD=30°;
(2)∵∠AED为△AEB的外角,且∠EAB=45°,∠DBG=30°,
∴∠AED=∠EAB+∠DBG=75°,
∵AB=DB,
∴∠BDA=∠BAD=
=75°,
∴∠ADE=∠AED,
∴AE=AD.
 证明:(1)过D作DG⊥AB,交AB于点G,
证明:(1)过D作DG⊥AB,交AB于点G,∵DC∥AB,
∴DG=CF,
∵△ABC为等腰直角三角形,且CF⊥AB,
∴CF为斜边AB上的中线,
∴CF=
| 1 |
| 2 |
∵AB=BD,
∴DG=
| 1 |
| 2 |
则在Rt△BDG中,∠ABD=30°;
(2)∵∠AED为△AEB的外角,且∠EAB=45°,∠DBG=30°,
∴∠AED=∠EAB+∠DBG=75°,
∵AB=DB,
∴∠BDA=∠BAD=
| 180°-30° |
| 2 |
∴∠ADE=∠AED,
∴AE=AD.
点评:此题考查了等腰直角三角形,平行线间的距离,含30度直角三角形的性质,以及等腰三角形的判定与性质,熟练掌握等腰直角三角形的性质是解本题的关键.

练习册系列答案
相关题目
已知△ABC∽△DEF,△ABC的面积为1,△DEF的面积为4,则△ABC与△DEF的周长之比为( )
| A、1:2 | B、1:4 |
| C、2:1 | D、4:1 |
 如图,点P与正方形ABCD的四个顶点都在⊙O的圆周上,则∠APB=( )
如图,点P与正方形ABCD的四个顶点都在⊙O的圆周上,则∠APB=( )| A、30° | B、45° |
| C、60° | D、90° |
 如图,是某立方体图形的展开图,则这个立体图形是( )
如图,是某立方体图形的展开图,则这个立体图形是( )| A、圆锥 | B、圆柱 | C、圆台 | D、球体 |
 如图,在直角坐标系xOy中,直线L:y=-x-1,双曲线y=
如图,在直角坐标系xOy中,直线L:y=-x-1,双曲线y= 如图,在平面直角坐标系内,以直线x=1为对称轴的抛物线y=ax2+bx-3与x轴相交于A、B两点,与y轴相交于点C,点A的坐标为(-1,0).
如图,在平面直角坐标系内,以直线x=1为对称轴的抛物线y=ax2+bx-3与x轴相交于A、B两点,与y轴相交于点C,点A的坐标为(-1,0).