题目内容
17．先化简，再求值：$（{\frac{1}{a-b}+\frac{1}{b+a}}）$÷$\frac{ab}{a+b}$．其中a=$\sqrt{2}$+1，b=1-$\sqrt{2}$．分析 先根据分式混合运算的法则把原式进行化简，再把a，b的值代入进行计算即可．
解答 解：原式=$\frac{a+b+a-b}{（a+b）（a-b）}$÷$\frac{ab}{a+b}$
=$\frac{2a}{（a+b）（a-b）}$•$\frac{a+b}{ab}$
=$\frac{2}{b（a-b）}$，
当a=$\sqrt{2}$+1，b=1-$\sqrt{2}$时，原式=$\frac{2（1-\sqrt{2}）}{\sqrt{2}+1-1+\sqrt{2}}$=$\frac{1-\sqrt{2}}{\sqrt{2}}$=$\frac{\sqrt{2}-2}{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
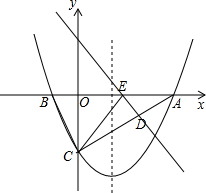已知：如图，对称轴为直线$x=\frac{3}{2}$的抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，连接BC、AC，且OB=$\frac{1}{2}$OA=$\frac{1}{3}$OC．
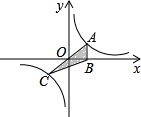如图．正比例函数y=kx与反比例函数y=$\frac{m}{x}$的图象相交于A（1，a）、C（b，-1）两点，过A作x轴的垂线交x轴于B，连BC．
如图，正方形ABCD、DEFH的边长都是5cm，点P从点D出发，先到点A，然后沿箭头所指方向运动（经过点D时不拐弯），则从出发开始连续运动2014cm时，它离点C 最近，此时它距该点1cm．