题目内容
2.已知方程x2+x-1=0,求一个一元二次方程x2-x-1=0,使它的根分别是已知方程根的倒数.分析 设x2+x-1=0的两根分别为a、b,根据根与系数的关系得到a+b=-1,ab=-1,再分别计算出$\frac{1}{a}$+$\frac{1}{b}$和$\frac{1}{a}$•$\frac{1}{b}$的值,然后根据根与系数的关系写出新方程.
解答 解:设x2+x-1=0的两根分别为a、b,
则a+b=-1,ab=-1,
所以$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{-1}{-1}$=1,
$\frac{1}{a}$•$\frac{1}{b}$=-1,
所以$\frac{1}{a}$和$\frac{1}{b}$为根的一元二次方程为x2-x-1=0.
故答案为x2-x-1=0.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.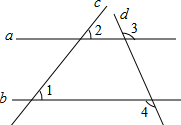 如图,若∠1=40°,∠2=40°,∠3=110°36′,则∠4的度数为( )
如图,若∠1=40°,∠2=40°,∠3=110°36′,则∠4的度数为( )
 如图,若∠1=40°,∠2=40°,∠3=110°36′,则∠4的度数为( )
如图,若∠1=40°,∠2=40°,∠3=110°36′,则∠4的度数为( )| A. | 68.6° | B. | 110°36′ | C. | 68.4° | D. | 69.4° |
12.若直线y=ax+b(a≠0)在第二、四象限都无图象,则抛物线y=ax2+bx+c( )
| A. | 开口向上,对称轴是y轴 | B. | 开口向下,对称轴平行于y轴 | ||
| C. | 开口向上,对称轴平行于y轴 | D. | 开口向下,对称轴是y轴 |
 如图,有长为24cm的篱笆,一面利用墙(墙长10m)围成中间隔道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为y(m2).
如图,有长为24cm的篱笆,一面利用墙(墙长10m)围成中间隔道篱笆的长方形花圃,设花圃的宽AB为x(m),面积为y(m2).
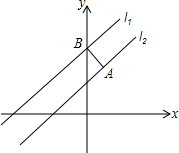 如图所示,已知两条直线l1:y=2x+7,l2:y=2x+5,在l2上任取一点A,过点A作直线l1的垂线,垂足为B点,求AB的长.
如图所示,已知两条直线l1:y=2x+7,l2:y=2x+5,在l2上任取一点A,过点A作直线l1的垂线,垂足为B点,求AB的长.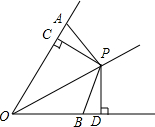 如图所示,P为∠AOB的平分线上一点,PC⊥OA于C,∠OAP+∠OBP=180°,若OC=4cm,求AO+OB的长.
如图所示,P为∠AOB的平分线上一点,PC⊥OA于C,∠OAP+∠OBP=180°,若OC=4cm,求AO+OB的长.