题目内容
6. 如图,长方形ABCD中,AB=4,BC=5,将长方形沿折痕AF折叠,点D恰好落在BC边上的点E处.
如图,长方形ABCD中,AB=4,BC=5,将长方形沿折痕AF折叠,点D恰好落在BC边上的点E处.(1)求BE的长;
(2)求CF的长.
分析 (1)根据矩形的性质得到AD=BC=5,∠D=∠B=∠C=90°,由折叠的性质得到AE=AD=BC=5,根据勾股定理即可得到结果;
(2)由(1)知BE=3,于是得到CE=BC-BE=2,根据折叠的性质得到EF=DF=4-CF,根据勾股定理即可得到结论.
解答 解:(1)长方形ABCD中,
∵AD=BC=5,∠D=∠B=∠C=90°,
∵△AEF是△ADF沿折痕AF折叠得到的,
∴AE=AD=BC=5,
∴BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3;
(2)由(1)知BE=3,
∴CE=BC-BE=2,
∵△AEF是△ADF沿折痕AF折叠得到的,
∴EF=DF=4-CF,
∵EF2=CE2+CF2,
∴(4-CF)2=22+CF2,
解得:CF=$\frac{3}{2}$.
点评 本题主要考查了图形的翻折变换,以及勾股定理、全等三角形、方程思想等知识,关键是熟练掌握勾股定理,找准对应边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知x1、x2是一元二次方程x2-4x+1=0的两个根,则x1•x2等于( )
| A. | -4 | B. | -1 | C. | 1 | D. | 4 |
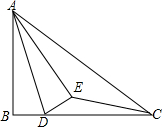 如图,已知在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是边BC上的任意一点,以AD为折痕翻折△ABD,使点B落在点E处,连接EC,当△DEC为直角三角形时,BD的长为3或6.
如图,已知在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是边BC上的任意一点,以AD为折痕翻折△ABD,使点B落在点E处,连接EC,当△DEC为直角三角形时,BD的长为3或6.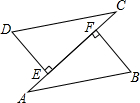 如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.
如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.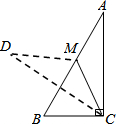 如图所示,在Rt△ABC中,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A=30°.
如图所示,在Rt△ABC中,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A=30°.