题目内容
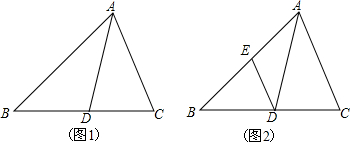
15. 如图所示,在Rt△ABC中,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A=30°.
如图所示,在Rt△ABC中,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A=30°.
分析 先根据折叠的性质得∠1=∠2,由CM为直角△ABC斜边上的中线,根据直角三角形斜边上的中线性质得MA=MC=MB,则∠1=∠A,根据三角形外角性质得∠3=∠1+∠A=2∠1=2∠2,再由CD⊥AB得到∠3+∠2=90°,根据三角形内角和定理可计算出∠2=30°,即可得到结果.
解答  解:如图,
解:如图,
∵△ABC的中线CM将△CMA折叠,使点A落在点D处,
∴∠1=∠2,
∵CM为直角△ABC斜边上的中线,
∴MA=MC=MB,
∴∠1=∠A,
∴∠2=∠A,∠3=∠1+∠A=2∠1=2∠2,
∵CD⊥AB,
∴∠3+∠2=90°,
∴2∠2+∠2=90°,
∴∠2=30°,
∴∠A=30°.
故答案为:30°.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了直角三角形斜边上的中线性质和等边三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,长方形ABCD中,AB=4,BC=5,将长方形沿折痕AF折叠,点D恰好落在BC边上的点E处.
如图,长方形ABCD中,AB=4,BC=5,将长方形沿折痕AF折叠,点D恰好落在BC边上的点E处.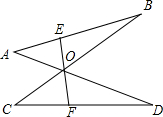 如图,AD、BC相交于点O,且OA=OC,OB=OD,EF过点O,分别交AB、CD于点E、F,且∠AOE=∠COF,求证:OE=OF.
如图,AD、BC相交于点O,且OA=OC,OB=OD,EF过点O,分别交AB、CD于点E、F,且∠AOE=∠COF,求证:OE=OF.