Question

4．点C在线段AB上，AC=8cm，CB=6cm，点M，N分别是AC，BC的中点．
（1）求线段MN的长．
（2）若C为线段AB上任一点，满足AC+CB=acm，其他条件不变，你能猜想MN的长度吗？并说明理由．
（3）若C在线段AB的延长线上，且满足AC-CB=bcm，M，N分别为AC，BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由．
拓展附加题：阅读下列材料并填空：
（1）探究：平面上有n个点（n≥2）且任意3个点不在同一条直线上，经过每两点画一条直线，一共能画多少条直线？
我们知道，两点确定一条直线．平面上有2个点时，可以画$\frac{2×1}{2}$=1条直线，平面内有3个点时，一共可以画$\frac{3×2}{2}$=3条直线，平面上有4个点时，一共可以画$\frac{4×3}{2}$=6条直线，平面内有5个点时，一共可以画10条直线，平面内有n个点时，一共可以画多少条直线？
（2）迁移：某足球联赛实行单循环比赛（每两队之间必须比赛一场），有2支球队时，要进行$\frac{2×1}{2}$=1场比赛，有3个球队时，要进行$\frac{3×2}{2}$=3场比赛，有4个球队时，要进行6场比赛，那么有20个球队时，要进行多少场比赛？

Answer 1

分析 （1）根据线段中点的性质，可得CM、CN的长，根据线段的和差，可得答案；
（2）根据线段中点的性质，可得CM、CN的长，根据线段的和差，可得答案；
（3）根据线段中点的性质，可得CM、CN的长，根据线段的和差，可得答案．

解答 解：（1）∵点M，N分别是AC，BC的中点，AC=8，CB=6，
∴CM=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4，CN=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3，
∴MN=CM+CN=4+3=7cm；
（2）∵点M，N分别是AC，BC的中点，
∴CM=$\frac{1}{2}$AC，CN=$\frac{1}{2}$BC，
∴MN=CM+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$（AC+BC）=$\frac{1}{2}$AB=$\frac{1}{2}$a（cm）；
（3）如图：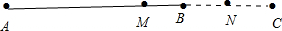
，
结论：MN=$\frac{1}{2}$b，
理由：∵点M，N分别是AC，BC的中点，AC=AB+BC
∴CM=$\frac{1}{2}$AC=$\frac{1}{2}$（AB+BC），CN=$\frac{1}{2}$BC，
∴MN=CM-CN=$\frac{1}{2}$（AC-BC）=$\frac{1}{2}$b（cm）
解：（1）当平面上有2个点时，可以画$\frac{2×1}{2}$=1条直线；
当平面上有3个点时，可以画$\frac{3×2}{2}$=3条直线；
…
当平面上有n（n≥2）个点时，可以画$\frac{n（n-1）}{2}$条直线；
因此当n=5时，一共可以画$\frac{5×4}{2}$=10条直线．
（2）同（1）可得：当比赛中有n（n≥2）个球队时，一共进行$\frac{n（n-1）}{2}$场比赛，
因此当n=4时，要进行$\frac{4×3}{2}$=6场比赛．当n=20时，要进行$\frac{20×19}{2}$=190场比赛．

点评 此题考查图形的变化规律，找出图形之间的联系，得出变化规律，解决问题．