题目内容
15.在△ABC中,∠A、∠B、∠C的度数的比是1:2:3,AB边上的中线长2cm,则△ABC的面积是2$\sqrt{3}$cm2.分析 设∠A=x°,∠B=2x°,∠C=3x°,由三角形内角和定理得出方程x+2x+3x=180,求出x,求出∠A=30°,∠B=60°,∠C=90°,再由AB边上的中线长2cm求出AB的长,由锐角三角函数的定义求出AC及BC的长,进而可得出结论.
解答 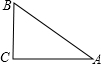 解:设∠A=x°,∠B=2x°,∠C=3x°,
解:设∠A=x°,∠B=2x°,∠C=3x°,
∵x+2x+3x=180,
∴x=30,
∴∠A=30°,∠B=60°,∠C=90°,即△ABC是直角三角形.
∵AB边上的中线长2cm,
∴AB=4cm,
∴BC=$\frac{1}{2}$AB=2cm,AC=AB•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$cm,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$(cm2).
故答案为:2$\sqrt{3}$cm2.
点评 本题考查的是直角三角形斜边上的中线,涉及到三角形的面积,含30度角的直角三角形性质,三角形的内角和定理等知识点,关键是求出三角形是直角三角形和求出AC和BC的长.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
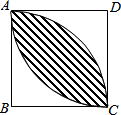 如图所示,若正方形边长为a,则阴影部分的面积为($\frac{1}{2}$π-1)a2.
如图所示,若正方形边长为a,则阴影部分的面积为($\frac{1}{2}$π-1)a2.