题目内容
2. 如图,AB=AC,∠A=36°,直线MN垂直平分AC交AB于M.
如图,AB=AC,∠A=36°,直线MN垂直平分AC交AB于M.(1)求∠BCM的度数;
(2)若AB=5,BC=3,求△BCM的周长.
分析 (1)由AB=AC,∠A=36°,可求得∠ACB的度数,又由直线MN垂直平分AC交AB于M,根据线段垂直平分线的性质,可求得AM=CM,即可求得∠ACM的度数,继而求得∠BCM的度数;
(2)由AM=CM,可得△BCM的周长=BC+AB.
解答 解:(1)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵直线MN垂直平分AC交AB于M,
∴AM=CM,
∴∠ACM=∠A=36°,
∴∠BCM=∠ACB-∠ACM=36°;
(2)∵AM=CM,
∴△BCM的周长=BC+CM+BM=BC+AM+BM=BC+AB=3+5=8.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
10.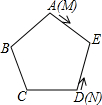 如图,M、N是正五边形ABCDE各边上的两个动点,若它们分别从顶点A、D出发,同时沿正五方形的边移动,M点以顺时针方向移动,N点以逆时针方向移动,假设点M的速度是点N的速度的5倍,则它们第2014次相遇在( )边上.
如图,M、N是正五边形ABCDE各边上的两个动点,若它们分别从顶点A、D出发,同时沿正五方形的边移动,M点以顺时针方向移动,N点以逆时针方向移动,假设点M的速度是点N的速度的5倍,则它们第2014次相遇在( )边上.
 如图,M、N是正五边形ABCDE各边上的两个动点,若它们分别从顶点A、D出发,同时沿正五方形的边移动,M点以顺时针方向移动,N点以逆时针方向移动,假设点M的速度是点N的速度的5倍,则它们第2014次相遇在( )边上.
如图,M、N是正五边形ABCDE各边上的两个动点,若它们分别从顶点A、D出发,同时沿正五方形的边移动,M点以顺时针方向移动,N点以逆时针方向移动,假设点M的速度是点N的速度的5倍,则它们第2014次相遇在( )边上.| A. | AE | B. | ED | C. | CD | D. | AB |
17.下列方程中,不是一元二次方程的是( )
| A. | x2=1 | B. | x(x-1)=x(x-2) | C. | x2+2=0 | D. | x(x-1)=x |
14.如果x<0,y<0,且3x-2y=$\sqrt{xy}$,则$\frac{x}{y}$的值为( )
| A. | -$\frac{4}{9}$ | B. | 1 | C. | $\frac{4}{9}$ | D. | 1或$\frac{4}{9}$ |

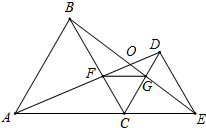 如图,点A,C,E在一条直线上,已知ABC和△EDC都是等边三角形,AD,BE相交于点O,AD,BC相交于点F,CD,BE相交于点G.连接FG和OC.
如图,点A,C,E在一条直线上,已知ABC和△EDC都是等边三角形,AD,BE相交于点O,AD,BC相交于点F,CD,BE相交于点G.连接FG和OC.