题目内容
9.下列各式中,最简分式是( )| A. | $\frac{34(x+y)}{85(x-y)}$ | B. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}y+x{y}^{2}}$ | ||
| C. | $\frac{{y}^{2}{-x}^{2}}{x+y}$ | D. | $\frac{(x+y)^{2}}{{y}^{2}-{x}^{2}}$ |
分析 最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答 解:A、A的分子分母有最大公约数17,不是最简分式;
B、B的分子、分母都不能再分解,且不能约分,是最简分式;
C、$\frac{{y}^{2}-{x}^{2}}{x+y}$=$\frac{(y+x)(y-x)}{x+y}$=y-x;
D、$\frac{(x+y)^{2}}{{y}^{2}-{x}^{2}}$=$\frac{(x+y)^{2}}{(y+x)(y-x)}$=$\frac{x+y}{y-x}$;
故选B.
点评 本题考查了最简分式,分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.

练习册系列答案
相关题目
19.数轴上原点以及原点右边的点所表示的数是( )
| A. | 负数 | B. | 非负数 | C. | 正数 | D. | 非正数 |
14.解方程:
(1)$\frac{x}{x-2}-\frac{2}{{x}^{2}-4}=1$
(2)$\frac{3}{x}-\frac{2}{1-x}=\frac{x+5}{{x}^{2}-x}$.
(1)$\frac{x}{x-2}-\frac{2}{{x}^{2}-4}=1$
(2)$\frac{3}{x}-\frac{2}{1-x}=\frac{x+5}{{x}^{2}-x}$.
1.已知抛物线y=ax2+bx+c经过原点和第二、三、四象限,则( )
| A. | a>0,b<0,c=0 | B. | a<0,b<0,c=0 | C. | a>0,b=c=0 | D. | a<0,b>0,c=0 |
18.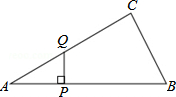 如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,当△APQ的面积为14$\sqrt{3}$时,则x的值为( )
如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,当△APQ的面积为14$\sqrt{3}$时,则x的值为( )
 如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,当△APQ的面积为14$\sqrt{3}$时,则x的值为( )
如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q.设AP=x,当△APQ的面积为14$\sqrt{3}$时,则x的值为( )| A. | 2$\sqrt{21}$ | B. | 2$\sqrt{21}$或14 | C. | 2或2$\sqrt{21}$或14 | D. | 2或14 |