题目内容
已知:在平面直角坐标系中,抛物线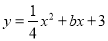 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
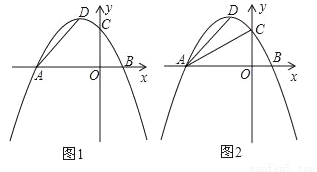
(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
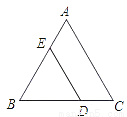
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
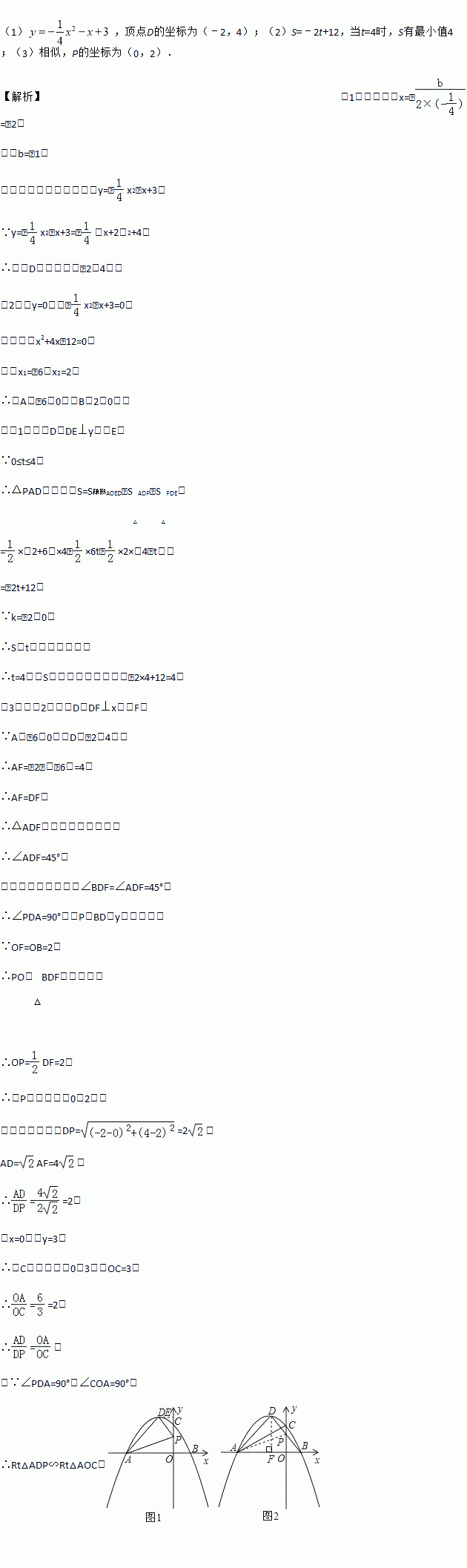
(1),顶点D的坐标为(﹣2,4);(2)S=﹣2t+12,当t=4时,S有最小值4;(3)相似,P的坐标为(0,2). 【解析】(1)对称轴为x=﹣=﹣2, 解得b=﹣1, 所以,抛物线的解析式为y=﹣x2﹣x+3, ∵y=﹣x2﹣x+3=﹣(x+2)2+4, ∴顶点D的坐标为(﹣2,4); (2)令y=0,则﹣x2﹣x+3=0, 整理得,x2+4x﹣1...
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目

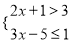 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )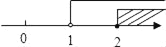 B.
B. 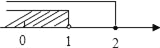
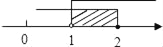 D.
D.