题目内容
探究与发现:
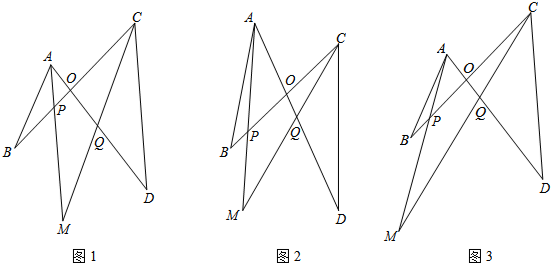
平面内,四条线段AB、BC、CD、DA首尾顺次相接,BC与AD相交于点O.
(1)如图1,若∠B=24°,∠D=42°,∠BAD和∠BCD的角平分线交于点M,求∠M的度数;
(2)如图2,若∠B=50°,∠D=32°,∠BAM=
∠BAD,∠BCM=
∠BCD,求∠M的度数;
(3)如图3,设∠B=x°,∠D=y°,∠BAM=
∠BAD,∠BCM=
∠BCD,用含n、x、y的代数式表示∠M的度数(直接写答案).
平面内,四条线段AB、BC、CD、DA首尾顺次相接,BC与AD相交于点O.
(1)如图1,若∠B=24°,∠D=42°,∠BAD和∠BCD的角平分线交于点M,求∠M的度数;
(2)如图2,若∠B=50°,∠D=32°,∠BAM=
| 1 |
| 3 |
| 1 |
| 3 |
(3)如图3,设∠B=x°,∠D=y°,∠BAM=
| 1 |
| n |
| 1 |
| n |

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据题意,设∠COD=x°,根据三角形的内角和定理以及角平分线的定义可以利用x表示出∠BCM的值,以及∠APB的度数,即∠CPM的度数,在△CPM中,利用三角形的内角和定理,即可求∠M.
(2)根据题意,设∠COD=x°,根据三角形的内角和定理以及∠BAM=
∠BAD,∠BCM=
∠BCD可以利用x表示出∠BCM的值,以及∠APB的度数,即∠CPM的度数,在△CPM中,利用三角形的内角和定理,即可求∠M.
(3)同理求出∠M.
(2)根据题意,设∠COD=x°,根据三角形的内角和定理以及∠BAM=
| 1 |
| 3 |
| 1 |
| 3 |
(3)同理求出∠M.
解答:(1):如图1,设∠COD=x°,则∠AOB=∠COD=x°,
△COD中∠BCD=180°-∠ADC-∠COD=180°-42°-x=138°-x,
∵CM平分∠BCD得到:
∠BCM=
∠BCD=69°-
x,
同理:∠BAM=∠MAD=78°-
x,
在△ABP中利用三角形内角和定理得到
∠APB=180°-24°-(78°-
x)=78°+
x,
则∠CPM=∠APB=180°-24°-(78°-
x)=78°+
x,
在△CPM中三内角的和是180°,
即:(69°-
x)+(78°+
x)+∠AMC=180°,
则∠AMC=33°;
(2)如图2:设∠COD=x°,则∠AOB=∠COD=x°,
△COD中∠BCD=180°-∠ADC-∠COD=180°-32°-x=148°-x,
∵CM平分∠BCD得到:
∠BCM=
∠BCD=
-
x,
同理:∠BAM=∠MAD=
-
x,
在△ABP中利用三角形内角和定理得到
∠APB=180°-50°-(
-
x)=
+
x,
则∠CPM=∠APB=180°-50°-(
-
x)=
+
x,
在△CPM中三内角的和是180°,
即:(
-
x)+(
+
x)+∠AMC=180°,
136°+∠AMC=180°
所以∠M=44°.
(3)
∠M=∠B+
(∠BAD-∠BCD)=∠B+
(∠D-∠B)=x+
(y-x)=
x+
y
△COD中∠BCD=180°-∠ADC-∠COD=180°-42°-x=138°-x,
∵CM平分∠BCD得到:
∠BCM=
| 1 |
| 2 |
| 1 |
| 2 |
同理:∠BAM=∠MAD=78°-
| 1 |
| 2 |
在△ABP中利用三角形内角和定理得到
∠APB=180°-24°-(78°-
| 1 |
| 2 |
| 1 |
| 2 |
则∠CPM=∠APB=180°-24°-(78°-
| 1 |
| 2 |
| 1 |
| 2 |
在△CPM中三内角的和是180°,
即:(69°-
| 1 |
| 2 |
| 1 |
| 2 |
则∠AMC=33°;
(2)如图2:设∠COD=x°,则∠AOB=∠COD=x°,
△COD中∠BCD=180°-∠ADC-∠COD=180°-32°-x=148°-x,
∵CM平分∠BCD得到:
∠BCM=
| 1 |
| 3 |
| 148° |
| 3 |
| 1 |
| 3 |
同理:∠BAM=∠MAD=
| 130° |
| 3 |
| 1 |
| 3 |
在△ABP中利用三角形内角和定理得到
∠APB=180°-50°-(
| 130° |
| 3 |
| 1 |
| 3 |
| 260° |
| 3 |
| 1 |
| 3 |
则∠CPM=∠APB=180°-50°-(
| 130° |
| 3 |
| 1 |
| 3 |
| 260° |
| 3 |
| 1 |
| 3 |
在△CPM中三内角的和是180°,
即:(
| 148° |
| 3 |
| 1 |
| 3 |
| 260° |
| 3 |
| 1 |
| 3 |
136°+∠AMC=180°
所以∠M=44°.
(3)
∠M=∠B+
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| n-1 |
| n |
| 1 |
| n |
点评:在解题过程中如果需要一个量的值时,可以先把它设出,在解题过程中用所设的未知数表示,设的量可能也不需求出.

练习册系列答案
相关题目
 如图所示,已知△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
如图所示,已知△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.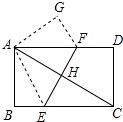 如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H. (1)阅读下面材料:
(1)阅读下面材料: