题目内容
5.在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字-1,-2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率.
分析 (1)通过列表展示所有9种等可能的结果数;
(2)找出满足点(x,y)落在函数y=-x+1的图象上的结果数,然后根据概率公式求解.
解答 解:(1)列表如下:
x y | 0 | 1 | 2 |
| -1 | (0,-1) | (1,-1) | (2,-1) |
| -2 | (0,-2) | (1,-2) | (2,-2) |
| 0 | (0,0) | (1,0) | (2,0) |
(2)满足点(x,y)落在函数y=-x+1的图象上的结果有2个,即(2,-1),( 1,0 ),
所以点M(x,y)在函数y=-x+1的图象上的概率=$\frac{2}{9}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
相关题目
15. 一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
 一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )| A. | 4 | B. | 5 | C. | 6$\sqrt{3}$ | D. | 6 |
 如图,AB是⊙O的直径,点P是弦AC上一个动点(不与A、C重合),PE⊥AB,点E为垂足,射线EP交$\widehat{AC}$于点F,交过点C的切线于点D.
如图,AB是⊙O的直径,点P是弦AC上一个动点(不与A、C重合),PE⊥AB,点E为垂足,射线EP交$\widehat{AC}$于点F,交过点C的切线于点D. 如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.
如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.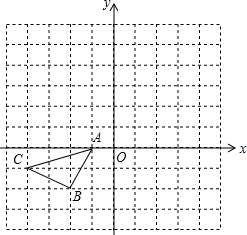 在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.
在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题. 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.