题目内容
14.已知⊙O的直径为10,点A、点B、点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD的长;
(2)如图②,若∠CAB=60°,CF⊥BD,①求证:CF是⊙O的切线;②求由弦CD、CB以及弧DB围成图形的面积.
分析 (1)利用圆周角定理可以判定△CAB和△DCB是直角三角形,利用勾股定理可以求得AC的长度;利用圆心角、弧、弦的关系推知△DCB也是等腰三角形,所以利用勾股定理同样得到BD=CD=5$\sqrt{2}$;
(2)①根据角平分线的性质得到∠CAD=30°,求得∠COD=60°,得到△COD是等边三角形,求得∠OCD=60°,得到∠FCD=30°,于是得到结论;②连接OB,根据圆周角定理得到∠BOD=60°,推出OC∥BD,得到S阴影=S扇形,根据扇形的面积公式即可得到结论.
解答 解:(Ⅰ)如图①,∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=8,
∵AD平分∠CAB,
∴$\widehat{CD}$=$\widehat{BD}$,
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,
∴易求BD=CD=5 $\sqrt{2}$;
(2)①证明:∵∠BAC=60°,AD平分∠CAB,
∴∠CAD=30°,
∴∠COD=60°,
∴△COD是等边三角形,
∴∠OCD=60°,
∵CF⊥BD,
∴∠CFD=90°,
∵∠CDF=∠CAB=60°,
∴∠FCD=30°,
∴∠OCF=∠OCD+∠DCF=90°,
∴OC⊥CF,
∴CF是⊙O的切线;
②连接OB,
∵∠BAD=$\frac{1}{2}∠$BAC=30°,
∴∠BOD=60°,
∴∠ODB=∠COD=60°,
∴OC∥BD,
∴S阴影=S扇形,
∵⊙O的直径为10,
∴OB=5,
∴S阴影=S扇形=$\frac{60•π×{5}^{2}}{360}$=$\frac{25}{6}$π.
点评 本题综合考查了圆周角定理,勾股定理以及等边三角形的判定与性质.此题利用了圆的定义、有一内角为60度的等腰三角形为等边三角形证得△OBD是等边三角形.

| A. | -3℃ | B. | -5℃ | C. | 5℃ | D. | -9℃ |
| A. | x3•(-x)3=(-x)6 | B. | x10÷x2=x5 | C. | (a+b)2=a2+b2 | D. | (2x3)2=4x6 |
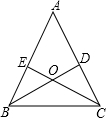 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.