题目内容
13. 如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.
如图,抛物线y=-x2+5x+n经过点A(1,0),与y轴交于点B.(1)求抛物线的解析式;
(2)求抛物线的对称轴和顶点坐标.
(3)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.
分析 (1)把点A的坐标代入解析式,计算即可;
(2)利用配方法把一般式化为顶点式,根据二次函数的性质解答;
(3)分PB=PA、PA=AB两种情况,根据等腰三角形的性质解答.
解答 解:(1)由题意得,-1+5+n=0,
解得,n=-4,
∴抛物线的解析式为y=-x2+5x-4;
(2)y=-x2+5x-4=-(x-$\frac{5}{2}$)2+$\frac{9}{4}$,
抛物线对称轴为:x=$\frac{5}{2}$,
顶点坐标为 ($\frac{5}{2}$,$\frac{9}{4}$);
(3)∵点A的坐标为(1,0),点B的坐标为(0,-4),
∴OA=1,OB=4,
在Rt△OAB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{17}$,
①当PB=PA时,PB=$\sqrt{17}$,
∴OP=PB-OB=$\sqrt{17}$-4,
此时点P的坐标为(0,$\sqrt{17}$-4),
②当PA=AB时,OP=OB=4
此时点P的坐标为(0,4).
点评 本题考查的是待定系数法求函数解析式、定义三角形的性质,掌握待定系数法求出函数解析式的一般步骤、灵活运用分情况讨论思想是解题的关键.

练习册系列答案
相关题目
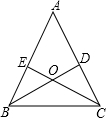 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
 如图是由六块积木搭成,这几块积木都是相同的正方体,请画出这个图形的三视图.
如图是由六块积木搭成,这几块积木都是相同的正方体,请画出这个图形的三视图.