题目内容
8. 如图,AB∥DE,CM平分∠BCE,CN⊥CM,猜想∠B与∠DCN的数量关系,并说明理由.
如图,AB∥DE,CM平分∠BCE,CN⊥CM,猜想∠B与∠DCN的数量关系,并说明理由.
分析 先根据平行线的性质得出∠B=∠BCD,再根据CM平分∠BCE可知∠1=∠2,再由CN⊥CM可知,∠2+∠3=90°,故∠1+∠4=90°,所以∠3=∠4,故可得出∠B=2∠DCN.
解答  解:∠B=2∠DCN,理由如下:
解:∠B=2∠DCN,理由如下:
∵AB∥DE,
∴∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
点评 本题考查的是平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了垂直的定义,角平分线定义以及平角的定义.

练习册系列答案
相关题目
16.在面积为60的?ABCD中,过点A作AE⊥直线BC于点E,作AF⊥直线CD于点F,若AB=10,BC=12,则CE+CF的值为( )
| A. | 22+11$\sqrt{3}$ | B. | 22-11$\sqrt{3}$ | C. | 22+11$\sqrt{3}$或22-11$\sqrt{3}$ | D. | 22+11$\sqrt{3}$或2+$\sqrt{3}$ |
3. 如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
 如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )| A. | 120° | B. | 128° | C. | 110° | D. | 100° |
13.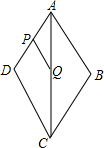 如图,菱形ABCD,∠B=120°,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的面积为( )
如图,菱形ABCD,∠B=120°,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的面积为( )
 如图,菱形ABCD,∠B=120°,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的面积为( )
如图,菱形ABCD,∠B=120°,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的面积为( )| A. | 6 | B. | 18$\sqrt{3}$ | C. | 24 | D. | 36$\sqrt{3}$ |
20.关于二次函数y=-(x+1)2+2的图象,下列判断正确的是( )
| A. | 图象开口向上 | B. | 图象的对称轴是直线x=1 | ||
| C. | 图象有最低点 | D. | 图象的顶点坐标为(-1,2) |
18.-8的立方根是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 不存在 |
 如图,已知∠1=50°,∠2=130°,且BD∥CE,AC与DF平行吗?为什么?
如图,已知∠1=50°,∠2=130°,且BD∥CE,AC与DF平行吗?为什么?