题目内容
8.观察下列等式:第一个等式:${a}_{1}=\frac{2}{1+3×2+2×{2}^{2}}=\frac{1}{2+1}-\frac{1}{{2}^{2}+1}$
第二个等式:${a}_{2}=\frac{{2}^{2}}{1+3×{2}^{2}+2×({2}^{2})^{2}}=\frac{1}{{2}^{2}+1}-\frac{1}{{2}^{3}+1}$
第三个等式:${a}_{3}=\frac{{2}^{3}}{1+3×{2}^{3}+2×({2}^{3})^{2}}=\frac{1}{{2}^{3}+1}-\frac{1}{{2}^{4}+1}$
第四个等式:${a}_{4}=\frac{{2}^{4}}{1+3×{2}^{4}+2×({2}^{4})^{2}}=\frac{1}{{2}^{4}+1}-\frac{1}{{2}^{5}+1}$
按上述规律,回答下列问题:
(1)请写出第六个等式:a6=$\frac{{2}^{6}}{1+3×{2}^{6}+2×({2}^{6})^{2}}$=$\frac{1}{{2}^{6}+1}$-$\frac{1}{{2}^{7}+1}$;
(2)用含n的代数式表示第n个等式:an=$\frac{{2}^{n}}{1+3×{2}^{n}+2×({2}^{n})^{2}}$=$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$;
(3)a1+a2+a3+a4+a5+a6=$\frac{14}{43}$(得出最简结果);
(4)计算:a1+a2+…+an.
分析 (1)根据已知4个等式可得;
(2)根据已知等式得出答案;
(3)利用所得等式的规律列出算式,然后两两相消,计算化简后的算式即可得;
(4)根据已知等式规律,列项相消求解可得.
解答 解:(1)由题意知,a6=$\frac{{2}^{6}}{1+3×{2}^{6}+2×({2}^{6})^{2}}$=$\frac{1}{{2}^{6}+1}$-$\frac{1}{{2}^{7}+1}$,
故答案为:$\frac{{2}^{6}}{1+3×{2}^{6}+2×({2}^{6})^{2}}$,$\frac{1}{{2}^{6}+1}$-$\frac{1}{{2}^{7}+1}$;
(2)an=$\frac{{2}^{n}}{1+3×{2}^{n}+2×({2}^{n})^{2}}$=$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$,
故答案为:$\frac{{2}^{n}}{1+3×{2}^{n}+2×({2}^{n})^{2}}$,$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$;
(3)原式=$\frac{1}{2+1}$-$\frac{1}{{2}^{2}+1}$+$\frac{1}{{2}^{2}+1}$-$\frac{1}{{2}^{3}+1}$+$\frac{1}{{2}^{3}+1}$-$\frac{1}{{2}^{4}+1}$+$\frac{1}{{2}^{4}+1}$-$\frac{1}{{2}^{5}+1}$+$\frac{1}{{2}^{5}+1}$-$\frac{1}{{2}^{6}+1}$+$\frac{1}{{2}^{6}+1}$-$\frac{1}{{2}^{7}+1}$
=$\frac{1}{2+1}$-$\frac{1}{{2}^{7}+1}$
=$\frac{14}{43}$,
故答案为:$\frac{14}{43}$;
(4)原式=$\frac{1}{2+1}$-$\frac{1}{{2}^{2}+1}$+$\frac{1}{{2}^{2}+1}$-$\frac{1}{{2}^{3}+1}$+…+$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$
=$\frac{1}{2+1}$-$\frac{1}{{2}^{n+1}+1}$
=$\frac{{2}^{n+1}-2}{3({2}^{n+1}+1)}$.
点评 本题主要考查数字的变化,解题的关键是根据已知等式得出等式的变化规律及列项相消法求解.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案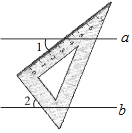 已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )
已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2的度数是( )| A. | 37° | B. | 53° | C. | 63° | D. | 27° |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
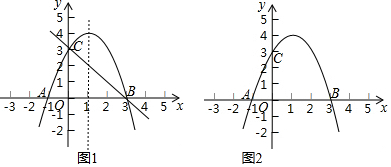
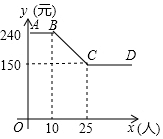 某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.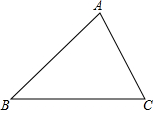 如图,已知△ABC中,AB=4,AC=3.
如图,已知△ABC中,AB=4,AC=3. 如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论: 如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在黑色区域的概率.
如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在黑色区域的概率.