题目内容
3.已知直线l:y=ax-a+2与x轴交于点A,与y轴交于点B,O点为坐标原点,△ABO外接圆的圆心为点C.设经过C点的反比例函数解析式为y=$\frac{k}{x}$,当点O到直线l距离最大时,k=$\frac{9}{4}$.分析 令x=0,则y=2-a,令y=0则x=$\frac{a-2}{a}$,得到A($\frac{a-2}{a}$,0),B(0,2-a),由△ABO外接圆的圆心为点C得到点C是AB的中点,求得C($\frac{a-2}{2a}$,$\frac{2-a}{2}$),当点O到直线l距离最大时,△ABC是等腰直角三角形,根据等腰直角三角形的性质得到AO=BO,于是得到结论.
解答 解:∵直线l:y=ax-a+2与x轴交于点A,与y轴交于点B,
令x=0,则y=2-a,令y=0则x=$\frac{a-2}{a}$,
∴A($\frac{a-2}{a}$,0),B(0,2-a),
∵O点为坐标原点,
∴∠AOB=90°,
∵△ABO外接圆的圆心为点C,
∴点C是AB的中点,
∴C($\frac{a-2}{2a}$,$\frac{2-a}{2}$),
当点O到直线l距离最大时,△ABC是等腰直角三角形,
∴AO=BO,
∴$\frac{a-2}{a}$=2-a,
解得:a=2或a=-1,
当a=-1时,C($\frac{3}{2}$,$\frac{3}{2}$),
∴k=$\frac{9}{4}$,
当a=2时,C(0,0)(不合题意,舍去)
∴k=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查了三角形的外接圆与外心,等腰直角三角形的性质,反比例函数图象上点的坐标特征,正确的理解题意是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
4.若数据10,9,a,12,9的平均数是10,则这组数据的方差是( )
| A. | 1 | B. | 1.2 | C. | 0.9 | D. | 1.4 |
12. 某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布表a=10,b=0.100,和频数分布直方图;
(2)这50个家庭电费支出的中位数落在哪个组内?
(3)若该地区有3万个家庭,请你估计该地区有多少个一年电费支出低于1400元的家庭?
 某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).| 分组/元 | 频 数 | 频 率 |
| 1000<x<1200 | 3 | 0.060 |
| 1200<x<1400 | 12 | 0.240 |
| 1400<x<1600 | 18 | 0.360 |
| 1600<x<1800 | a | 0.200 |
| 1800<x<2000 | 5 | b |
| 2000<x<2200 | 2 | 0.040 |
| 合计 | 50 | 1.000 |
(1)补全频数分布表a=10,b=0.100,和频数分布直方图;
(2)这50个家庭电费支出的中位数落在哪个组内?
(3)若该地区有3万个家庭,请你估计该地区有多少个一年电费支出低于1400元的家庭?
13.“约在江苏,共筑梦想”,为了解某校1000名学生在2017年5月20日“江苏发展大会”期间对会议的关注方式,某班兴趣小组随机抽取了部分学生进行问卷调查,某校抽取学生“江苏发展大会”期间对会议的关注方式的统计表并将问卷调查的结果绘制成如下不完整的统计表:
(1)本次问卷调查抽取的学生共有50人,其中通过电视关注会议的学生有8人;
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过报纸关注会议的约有多少人?
| 方式 | 频数 | 百分比 |
| 网络 | 23 | 46% |
| 电视 | ||
| 报纸 | 8% | |
| 其他 | 15 | |
| 合计 | 100% |
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过报纸关注会议的约有多少人?
 如图是一个由三个相同正方体组成的立体图形,它的主视图是( )
如图是一个由三个相同正方体组成的立体图形,它的主视图是( )



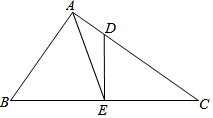 如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.
如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.