题目内容
15.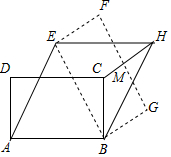 如图,矩形ABCD中,AB=3,AD=$\sqrt{3}$,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
如图,矩形ABCD中,AB=3,AD=$\sqrt{3}$,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由旋转的性质得到AB=BE,根据菱形的性质得到AE=AB,推出△ABE是等边三角形,得到AB=3,AD=$\sqrt{3}$,根据三角函数的定义得到∠BAC=30°,求得AC⊥BE,推出C在对角线AH上,得到A,C,H共线,于是得到结论.
解答 解:∵将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,
∴AB=BE,
∵四边形AEHB为菱形,
∴AE=AB,
∴AB=AE=BE,
∴△ABE是等边三角形,
∵AB=3,AD=$\sqrt{3}$,
∴tan∠CAB=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{3}$,
∴∠BAC=30°,
∴AC⊥BE,
∴C在对角线AH上,
∴A,C,H共线,
∴AO=OH=$\frac{\sqrt{3}}{2}$AB=$\frac{3\sqrt{3}}{2}$,
∵OC=$\frac{1}{2}$BC=$\frac{\sqrt{3}}{2}$,
∵∠COB=∠OBG=∠G=90°,
∴四边形OBGM是矩形,
∴OM=BG=BC=$\sqrt{3}$,
∴HM=OH-OM=$\frac{\sqrt{3}}{2}$
故选D.
点评 本题考查了旋转的性质,矩形的性质,解直角三角形,菱形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
7.化简:-$\sqrt{(1-sin52°)^{2}}$-$\sqrt{(1-tan52°)^{2}}$的结果是( )
| A. | tan52°-sin52° | B. | sin52°-tan52° | C. | 2-sin52°-tan52° | D. | -sin52°-tan52° |
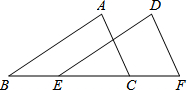 如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7.
如图,已知△ABC≌△DEF,点B,E,C,F在同一条直线上,若BC=5,BE=2,则BF=7.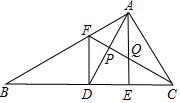 如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论
如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论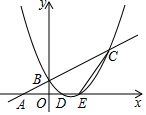 已知:如图一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
已知:如图一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)