题目内容
20. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S△ABC=2S△ABF.其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S△ABC=2S△ABF.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①根据四边形ABCD是矩形,BE⊥AC,可得∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB,故①正确;
②根据点E是AD边的中点,以及AD∥BC,得出△AEF∽△CBF,根据相似三角形对应边成比例,可得CF=2AF,故②正确;
③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=$\frac{1}{2}$BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故③正确;
④根据CF=2AF,即可得出结论④错误;即可得出结论.
解答 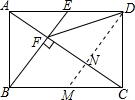 解:如图,过D作DM∥BE交AC于N,交BC于M,
解:如图,过D作DM∥BE交AC于N,交BC于M,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∴∠EAC=∠ACB,
∵BE⊥AC于点F,
∴∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴$\frac{AE}{BC}=\frac{AF}{FC}$=$\frac{1}{2}$,
∵AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴$\frac{AF}{CF}$=$\frac{1}{2}$,
∴CF=2AF,故②正确;
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=$\frac{1}{2}$BC,
∴BM=CM,CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DN垂直平分CF,
∴DF=DC,故③正确;
∵CF=2AF,
∴S△ABC=3S△ABF.
∴④不正确;
其中正确的结论有3个,
故选:B.
点评 本题考查了相似三角形的判定和性质,矩形的性质,相似三角形的判定与性质,图形面积的计算的综合应用,正确作出辅助线是解题的关键.解题时注意,相似三角形的对应边成比例.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
10.方程2-x=-2的解是( )
| A. | x=1 | B. | x=-4 | C. | x=4 | D. | x=0 |
11.下列图形都是用同样大小的黑点按一定规律组成的,其中第1个图形有1个黑点,第2个图形有3个黑点,第3个图形有7个黑点,第4个图形有13个黑点,…则第9个图形中黑点的个数是( )


| A. | 43 | B. | 57 | C. | 64 | D. | 73 |
8.在下列说法中:
(1)△ABC在平移过程中,对应线段一定相等
(2)△ABC在平移过程中,对应线段一定平行
(3)△ABC在平移过程中,周长保持不变
(4)△ABC在平移过程中,对应边中点的连线段的长等于平移的距离
(5)△ABC在平移过程中,面积不变.
其中正确的有( )
(1)△ABC在平移过程中,对应线段一定相等
(2)△ABC在平移过程中,对应线段一定平行
(3)△ABC在平移过程中,周长保持不变
(4)△ABC在平移过程中,对应边中点的连线段的长等于平移的距离
(5)△ABC在平移过程中,面积不变.
其中正确的有( )
| A. | (1)(2)(3)(4) | B. | (1)(2)(3)(4)(5) | C. | (1)(2)(3)(5) | D. | (1)(3)(4)(5) |
15.已知不等式组$\left\{\begin{array}{l}x>-a\\ x≥-b\end{array}$的解为x≥-b,则下列各式正确的是( )
| A. | a>b | B. | a<b | C. | b≤a | D. | a≤b |
10.不等式组$\left\{\begin{array}{l}{-2x<6}\\{x-2>0}\end{array}\right.$的解集是( )
| A. | x>-3 | B. | x<-3 | C. | x>2 | D. | 无解 |