题目内容
1.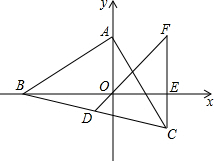 已知:点A(0,a)在y轴正半轴上,且满足$\sqrt{a-3}$+3$\sqrt{3-a}$=b+5,B为x轴上一动点,以AB为边作等腰Rt△ABC,AB=AC,∠BAC=90°,过点C作CE⊥x轴于E,当点B运动时,D为BC的中点,连接DO并延长交CE延长线于点F,求证:$\frac{BO}{CF}$为定值.
已知:点A(0,a)在y轴正半轴上,且满足$\sqrt{a-3}$+3$\sqrt{3-a}$=b+5,B为x轴上一动点,以AB为边作等腰Rt△ABC,AB=AC,∠BAC=90°,过点C作CE⊥x轴于E,当点B运动时,D为BC的中点,连接DO并延长交CE延长线于点F,求证:$\frac{BO}{CF}$为定值.
分析 如图,连接AD交OB于K,连接AF,由△AKO∽△BKD,推出$\frac{AK}{BK}$=$\frac{OK}{KD}$,推出$\frac{AK}{OK}$=$\frac{BK}{KD}$,推出△AKB≌△OKD,推出∠BAK=∠KOD=∠FOE=45°,∠ABK=∠KDO,同法由△AGD∽△FGC,推出△AGF∽△DGC,推出∠AFC=90°,再证明△ABO≌△ACF即可解决问题.
解答 证明:如图,连接AD交OB于K,连接AF.
∵∠BAC=90°,AB=AC,BD=DC,
∴AD=DB=DC,
∴∠ACD=∠BAD=∠DAC=45°,
∵∠AKO=∠BKD,∠AOK=∠BDK,
∴△AKO∽△BKD,
∴$\frac{AK}{BK}$=$\frac{OK}{KD}$,
∴$\frac{AK}{OK}$=$\frac{BK}{KD}$,∵∠AKB=∠DKO,
∴△AKB≌△OKD,
∴∠BAK=∠KOD=∠FOE=45°,∠ABK=∠KDO,
∵∠CF⊥x轴,
∴∠OFE=45°,
∵∠GAD=∠GFC,∠AGD=∠CGF,
∴△AGD∽△FGC,
∴$\frac{AG}{GF}$=$\frac{DG}{GC}$,∠ADG=∠GCF,
∴$\frac{AG}{DG}$=$\frac{FG}{GC}$,∵∠AGF=∠DGC,
∴△AGF∽△DGC,
∴∠AFG=∠GCD=45°,
∴∠AFC=90°,
∵∠ABO=∠ACF,∠AOB=∠AFC,AB=AC,
∴△ABO≌△ACF,
∴OB=CF,
∴$\frac{OB}{CF}$=1=定值.
点评 本题考查相似三角形的判定和性质、全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.某工厂2015年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2017年该产品的产量为y吨,则y关于x的函数关系式为( )
| A. | y=100(1-x)2 | B. | y=100(1+x)2 | ||
| C. | y=$\frac{100}{(1+x)^{2}}$ | D. | y=100+100(1+x)+100(1+x)2 |
18.若关于x的一元一次不等式组$\left\{\begin{array}{l}{2x-1>3(x-2)}\\{x<m}\end{array}\right.$的解集是x<5,则m的取值范围是( )
| A. | m≥5 | B. | m>5 | C. | m≤5 | D. | m<5 |
6.下列各式中,不能应用平方差公式进行计算的是( )
| A. | (a+b)(a-b) | B. | (x+2y)(x-2y) | C. | (-a-3)(-a+3) | D. | (2a-b)(-2a+b) |
13.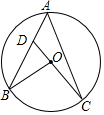 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠BDC的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠BDC的度数为( )
 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠BDC的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠BDC的度数为( )| A. | 60° | B. | 70° | C. | 75° | D. | 80° |
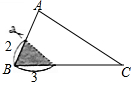
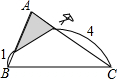
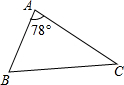 如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )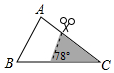

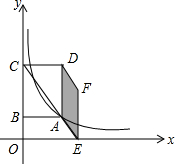 如图所示,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其它部分均在第一象限,双曲线y=$\frac{k}{x}$过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为4,则k值为( )
如图所示,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其它部分均在第一象限,双曲线y=$\frac{k}{x}$过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为4,则k值为( )