题目内容
17.下列各组中的两项属于同类项的是( )| A. | $\frac{5}{2}$ x2y与-$\frac{3}{2}$ xy3 | B. | -8a2b与5a2c | C. | $\frac{1}{4}$ pq与-$\frac{5}{2}$ qp | D. | 19abc与-28ab |
分析 根据同类项的定义对四个选项进行逐一分析即可.
解答 解:A、$\frac{5}{2}$x2y与-$\frac{3}{2}$xy3中所含字母的指数不同,不是同类项,故A错误;
B、-8a2b与5a2c中所含字母不同,不是同类项,故B错误;
C、$\frac{1}{4}$pq与-$\frac{5}{2}$qp中所含字母相同,相同字母的指数也相同,是同类项,故C正确;
D、19abc与-28ab中所含字母不同,不是同类项,故D错误.
故选:C.
点评 本题考查的是同类项的定义,解答此类题目时要注意判断同类项的依据:①一是所含字母相同,二是相同字母的指数也相同,两者缺一不可;②同类项与系数的大小无关;③同类项与它们所含的字母顺序无关;④所有常数项都是同类项.

练习册系列答案
相关题目
8.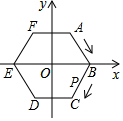 如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )
如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )
 如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )
如图,在平面直角坐标系中,六边形ABCDEF是半径为1的正六边形,点O为正六边形ABCDEF的中心,点P从点B出发,沿正六边形按顺时针方向运动,速度为每秒1个单位长度,则第2017秒时,点P的坐标是( )| A. | ($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | B. | (-1,0) | C. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | D. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) |
5.有理数$\frac{1}{3}$的相反数是( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | -$\frac{1}{3}$ |
12.某城市2012年底已有绿化面积200公顷,经过两年绿化,绿化面积逐年增加,到2014年底增加到288公顷.设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )
| A. | 200(1+x)=288 | B. | 288(1-x)2=200 | C. | 200(1+2x)=288 | D. | 200(1+x)2=288 |
9. 如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )
如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )
 如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )
如图,直线a∥b,直线c与直线a、b分别相交于点A、B,AD⊥b,垂足为D,若∠1=37°,则∠2=( )| A. | 53° | B. | 63° | C. | 37° | D. | 67° |
6.不等式组$\left\{\begin{array}{l}\frac{1}{2}x-1<\frac{x}{3}\;,\;\;\\ 2x-4<3x+3.\end{array}\right.$的解集为( )
| A. | -7<x<6 | B. | -7<x<1 | C. | x<1 | D. | x<6 |
7.-$\frac{1}{3}$的倒数是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
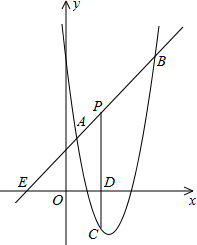 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.