题目内容
已知直线y=kx中,y随x的增大而减小,那么直线y=kx经过 象限.
考点:正比例函数的性质
专题:
分析:根据函数y=kx,y随x的增大而减小,得到k<0,从而确定正比例函数y=kx经过的象限.
解答:解:∵直线y=kx中,y随x的增大而减小,
∴k<0,
∴直线y=kx经过二、四象限,
故答案为:二、四.
∴k<0,
∴直线y=kx经过二、四象限,
故答案为:二、四.
点评:此题主要考查了正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.

练习册系列答案
相关题目
下列各式能用平方差公式分解因式的是( )
| A、-x2-y2 |
| B、(-x)2-y2 |
| C、(-x)2+y2 |
| D、x2+(-y)2 |
在平面直角坐标系中,点P(5,-2014)在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
在下列四个图形中,△DEF能由△ABC经过平移得到的图形是( )
A、 |
B、 |
C、 |
D、 |
已知点P(2-4m,m-2)在第二象限,则m的取值范围是( )
A、m>
| ||
| B、m<2 | ||
| C、m>2 | ||
D、
|
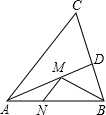 选做题:如图,在锐角△ABC中,AB=2,∠BAC=60°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是
选做题:如图,在锐角△ABC中,AB=2,∠BAC=60°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=
如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=