题目内容
1.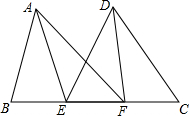 已知:点B,E,F,C在同一条直线上,AB=CD,BF=CE,AE=DF.求证:AF=DE.
已知:点B,E,F,C在同一条直线上,AB=CD,BF=CE,AE=DF.求证:AF=DE.
分析 根据BF=CE,得到BE=CF,证明△ABE≌△CDF,得到∠AEB=∠DFC,所以180°-∠AEB=180°-∠DFC,即∠AEF=∠DFE,证明△AEF≌△DFE,得到AF=DE.
解答 解:∵BF=CE,
∴BF-EF=CE-EF,
即BE=CF,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{AB=CD}\\{BE=CF}\\{AE=DF}\end{array}\right.$
∴△ABE≌△CDF,
∴∠AEB=∠DFC,
∴180°-∠AEB=180°-∠DFC,
即∠AEF=∠DFE,
在△AEF和△DFE中,
$\left\{\begin{array}{l}{AE=DF}\\{∠AEF=∠DFE}\\{EF=EF}\end{array}\right.$
∴△AEF≌△DFE,
∴AF=DE.
点评 本题考查了全等三角形的判定定理和性质定理,解决本题的关键是证明△ABE≌△CDF,△AEF≌△DFE.

练习册系列答案
相关题目
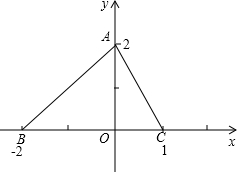 已知△ABC的顶点坐标分别为A(0,2),B(-2,0),C(1,0),O为坐标原点,试在AB和AC边上分别找一点D,E,使△DOE的周长最短,画出点D,E两点的位置图形,简述作图方法.
已知△ABC的顶点坐标分别为A(0,2),B(-2,0),C(1,0),O为坐标原点,试在AB和AC边上分别找一点D,E,使△DOE的周长最短,画出点D,E两点的位置图形,简述作图方法.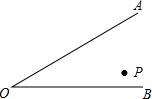 如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P1、P2分别在OA、OB上,求作点P1、P2,使△PP1P2的周长最小,连接OP,若OP=10cm,求△PP1P2的周长.
如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P1、P2分别在OA、OB上,求作点P1、P2,使△PP1P2的周长最小,连接OP,若OP=10cm,求△PP1P2的周长.
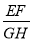 的值是( )
的值是( )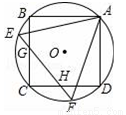
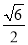 B.
B. 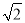 C.
C. 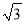 D. 2
D. 2