题目内容
4.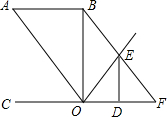 如图,已知AB∥CF,O为直线CF上一点,且OB平分∠AOE,ED⊥CF于D,且∠OBF=∠OED,∠BFC=∠A,那么OB和CF有怎样的位置关系?为什么?
如图,已知AB∥CF,O为直线CF上一点,且OB平分∠AOE,ED⊥CF于D,且∠OBF=∠OED,∠BFC=∠A,那么OB和CF有怎样的位置关系?为什么?
分析 先根据AB∥CD得出∠AOC=∠A,再由∠BFC=∠A可知∠AOC=∠BFC,故OA∥BF,所以∠AOB=∠OBF,再根据OB平分∠AOE可知∠AOB=∠BOE,故∠BOE=∠OBF,根据∠OBF=∠OED可得出∠OED=∠BOE,故可得出OB∥DE,再由ED⊥CF即可得出结论.
解答 解:ED⊥CF.
理由:∵AB∥CD,
∴∠AOC=∠A.
∵∠BFC=∠A,
∴∠AOC=∠BFC,
∴OA∥BF,
∴∠AOB=∠OBF.
∵OB平分∠AOE,
∴∠AOB=∠BOE,
∴∠BOE=∠OBF.
∵∠OBF=∠OED,
∴∠OED=∠BOE,
∴OB∥DE,
∵ED⊥CF,
∴ED⊥CF.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.$\root{3}{-8}$等于( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | -$\frac{1}{2}$ | D. | -2 |



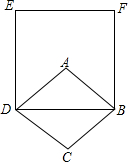 如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48.
如图,菱形ABCD中,∠ABC=60°,AB=4,则以BD为边长的正方形BDEF的面积为48.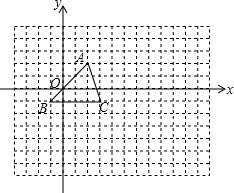 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立如图所示的平面直角坐标系后,△ABC的顶点均在格点上,且坐标分别为:A(2,2),B(-1,-1),C(3,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立如图所示的平面直角坐标系后,△ABC的顶点均在格点上,且坐标分别为:A(2,2),B(-1,-1),C(3,-1). 如图,△ABC按顺时针方向旋转36°得到△EDC,且点D在A上,如果AB=AC,
如图,△ABC按顺时针方向旋转36°得到△EDC,且点D在A上,如果AB=AC,