题目内容
2.已知:C为线段AB上任意一点,M是AC的中点,N是BC的中点.(1)若AB=10cm,AC=4cm,求MN的长;
(2)若AB=a,求MN的长;
(3)点C在AB上移动时,其他已知条件不变,此时MN的长是否改变?为什么?
分析 (1)先求得BC的长,然后根据中点的定义求得MC和CN的长,从而可求得MN的长;
(2)(3)根据中点的定义可知:MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}BC$,然后根据MN=MC+NC=$\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}AB$求解即可.
解答 解:(1)如图所示:
BC=AB-AC=10-4=6cm,
∵M是AC的中点,N是BC的中点,
∴MC=$\frac{1}{2}AC=\frac{1}{2}×4$=2,NC=$\frac{1}{2}CB=\frac{1}{2}×6$=3,
∴MN=MC+CN=2+3=5cm;
(2)∵M是AC的中点,N是BC的中点,
MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}BC$
∴MN=MC+NC=$\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}AB=\frac{1}{2}a$,
(3)当点C在AB上移动时,MN的长不变.
∵M是AC的中点,N是BC的中点,
MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}BC$
∴MN=MC+NC=$\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}AB$.
点评 本题主要考查的是线段的中点的定义,根据线段中点的定义得到:MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}BC$,从而得出MN=$\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}AB$是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
7.小亮的妈妈每天早上要送新鲜蔬菜到市场去卖,下表是上周送出的20筐新鲜蔬菜的质量记录,每筐以25千克为标准重量,求上周送出20筐新鲜蔬菜的总重量.
| 筐 数 | 2 | 5 | 3 | 4 | 2 | 4 |
| 与标准重量比较(千克) | -0.8 | +0.6 | -0.5 | -0.4 | +0.5 | -0.3 |
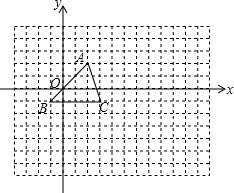 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立如图所示的平面直角坐标系后,△ABC的顶点均在格点上,且坐标分别为:A(2,2),B(-1,-1),C(3,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立如图所示的平面直角坐标系后,△ABC的顶点均在格点上,且坐标分别为:A(2,2),B(-1,-1),C(3,-1).