Question

3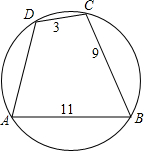．已知圆内接四边形ABCD中，AB=11，BC=9，CD=3，如图，$\widehat{AB}$+$\widehat{CD}$=$\widehat{BC}$+$\widehat{AD}$，则AD=7．

Answer 1

分析 作⊙O的直径AE，连接BE，DE，根据已知条件得到$\widehat{BE}$=$\widehat{CD}$，于是求得BE=CD=3，同理DE=BC=9，然后根据勾股定理列方程即可得到结论．

解答 解：作⊙O的直径AE，连接BE，DE，
∵$\widehat{AB}$+$\widehat{CD}$=$\widehat{BC}$+$\widehat{AD}$，
∴$\widehat{AB}$+$\widehat{CD}$=$\widehat{AB}$+$\widehat{BE}$，
∴$\widehat{BE}$=$\widehat{CD}$，
∴BE=CD=3，
同理DE=BC=9，
∵AE是⊙O的直径，
∴∠ABE=∠ADE=90°，
∴AB²+BE²=AD²+DE²，
即11²+3²=AD²+9²，
解得：AD=7．
故答案为：7．

点评 本题考查了圆心角、弧、弦的关系，圆周角定理，勾股定理，正确的作出辅助线是解题的关键．