题目内容
17. 如图,是药品研究所所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)随用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物就失去疗效,那么成人用药后需要多长时间血液中药物浓度才能达到最大值?
如图,是药品研究所所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)随用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物就失去疗效,那么成人用药后需要多长时间血液中药物浓度才能达到最大值?
分析 利用待定系数法分别求出直线OA与双曲线的函数解析式,再令它们相等得出方程,解方程即可求解.
解答 解:设直线OA的解析式为y=kx,
把(4,a)代入,得a=4k,解得k=$\frac{a}{4}$,
即直线OA的解析式为y=$\frac{a}{4}$x.
根据题意,(9,a)在反比例函数的图象上,
则反比例函数的解析式为y=$\frac{9a}{x}$.
当$\frac{a}{4}$x=$\frac{9a}{x}$时,解得x=±6(负值舍去),
故成人用药后,血液中药物则至少需要6小时达到最大浓度.
点评 本题考查了反比例函数的应用,直线与双曲线交点的求法,利用待定系数法求出关系式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7. 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )
 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2于点B,AC⊥l1于点A,AB=4,AC=5,则下列说法正确的是( )| A. | 点B到直线l1的距离等于4 | B. | 点A到直线l2的距离等于5 | ||
| C. | 点B到直线l1的距离等于5 | D. | 点C到直线l1的距离等于5 |
5.下列多项式乘法中,可用平方差公式计算的是( )
| A. | (2a+b)(2a-3b) | B. | (x-2y)(x+2y) | C. | (x+1)(1+x) | D. | (-x-y)(x+y) |
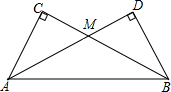 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,MC=4cm,则点M到直线AB的距离为4cm.
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,MC=4cm,则点M到直线AB的距离为4cm. 如图,点E在以AB为直径的⊙O上,点C是$\widehat{BE}$的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
如图,点E在以AB为直径的⊙O上,点C是$\widehat{BE}$的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.