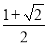��Ŀ����
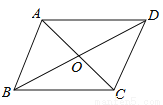
��ͼ��ƽ���ı���ABCD�У���E��F��G��H�ֱ���AB��BC��CD��AD������AE=CG��AH=CF��
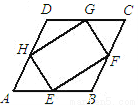
��1����֤���ı���EFGH��ƽ���ı��Σ�
��2�����AB=AD����AH=AE����֤���ı���EFGH�Ǿ��Σ�
��1��֤��������.��2��֤��������. �������������������1����֤�á�AEH�ա�CGF���Ӷ�֤��BE=DG��DH=BF�����У���BEF�ա�DGH����������Ա߷ֱ���ȵ��ı�����ƽ���ı��ζ���֤�� ��2��������֪��ƽ���ı���ABCD�����Σ�����AC��BD������AC��BD����AB=AD����AH=AE��֤��HE��BD��ͬ���ɵõ�HG��AC����HG��HE�����ɣ�1��֪�ı���HGFE��ƽ���ı���...
��ϰ��ϵ�д�
 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
�����Ŀ


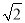 ��2
��2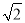 ��a��b������a��b�Ƿ���
��a��b������a��b�Ƿ���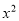 -2x-1=0��������������4�����ݵ���λ���ǣ�������
-2x-1=0��������������4�����ݵ���λ���ǣ�������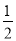 C. 2 D.
C. 2 D.