题目内容
如图，两幢建筑物的水平距离为32.6m，从点A测得点D的俯角α=35°12′，测得点C的俯角β为43°24′，求这两幢建筑物的高（结果精确到0.1m）．考点：解直角三角形的应用-仰角俯角问题
专题：
分析：首先分析图形：延长CD与水平线交于点E，根据题意构造直角三角形；本题涉及两个直角三角形，应利用其公共边构造关系式，进而可求出答案．
解答：
解：延长CD与水平线交于点E，
∵AE∥BC，
∴∠EAC=∠ACB=43°24′，
∵∠B=90°，
∴AB=BC÷tan46°36′=32.6÷1.06≈30.8（m），
在Rt△ADE中，DE=AEtan∠EAD=32.6×tan35°12′≈23.0（m），
∴CD=CE-DE=30.8-23.0=7.8（m）．
答：建筑物AB的高约为30.8m、CD的高约为7.8m．
解：延长CD与水平线交于点E，∵AE∥BC，
∴∠EAC=∠ACB=43°24′，
∵∠B=90°，
∴AB=BC÷tan46°36′=32.6÷1.06≈30.8（m），
在Rt△ADE中，DE=AEtan∠EAD=32.6×tan35°12′≈23.0（m），
∴CD=CE-DE=30.8-23.0=7.8（m）．
答：建筑物AB的高约为30.8m、CD的高约为7.8m．
点评：本题考查直角三角形的解法，首先构造直角三角形，再借助角边关系、三角函数的定义解题．
练习册系列答案
相关题目
如图，在Rt△AOB中，∠B=40°，以OA为半径，O为圆心作⊙O，交AB于点C，交OB于点D．求
把图①按一定比例缩小为图②（图②中的一条线段是图①长方形按比例缩小后的长），请你把图②补画完整．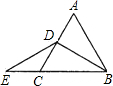
已知：如图，△ABC是等边三角形，BD是AC边上的高，延长BC到E，使CE=CD．求证：点D在BE的垂直平分线上．