��Ŀ����
5��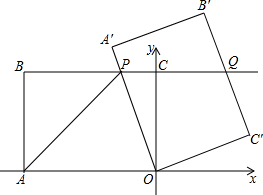 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ��-8��0����ֱ��BC������B��-8��6����C��0��6�������ı���OABC�Ƶ�O��˳ʱ�뷽����ת�ǶȦ��õ��ı���OA��B��C�䣬��ʱ��OA�����BC���ڵ�P����B��C����BC���ӳ��߽��ڵ�Q������AP��
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ��-8��0����ֱ��BC������B��-8��6����C��0��6�������ı���OABC�Ƶ�O��˳ʱ�뷽����ת�ǶȦ��õ��ı���OA��B��C�䣬��ʱ��OA�����BC���ڵ�P����B��C����BC���ӳ��߽��ڵ�Q������AP����1���ı���OABC����״�Ǿ��Σ�
��2������ת�����У�����PAO=��POA����P�����꣮
��3������ת�����У���PΪ�߶�BQ�е�ʱ������OQ�����OPQ�������
���� ��1������A��B��C������ó���COA=��OAB=��B=90�㣬�����ó��𰸣�
��2�����á�PAO=��POA�ó�PA=PO�������ó�AE=EO=4�����ɵó�P�����ꣻ
��3�����ȵó�Rt��OCQ��Rt��OC'Q��HL������������ƽ���ߵ����������POQ=��PQO�����ɵó�BP=PO�������ù��ɶ����ó�PQ�ij������������OPQ�������
���  �⣺��1���ߵ�A������Ϊ��-8��0������B��-8��6����C��0��6����
�⣺��1���ߵ�A������Ϊ��-8��0������B��-8��6����C��0��6����
���COA=��OAB=��B=90�㣬
���ı���OABC�Ǿ��Σ�
�ʴ�Ϊ�����Σ�
��2����ͼ1������P��PE��AO�ڵ�E��
�ߡ�PAO=��POA��
��PA=PO��
��PE��AO��
��AE=EO=4��
��P��-4��6����
��3����ͼ2����Rt��OCQ��Rt��OC'Q�У�
$\left\{\begin{array}{l}{CO=CO}\\{OQ=OQ}\end{array}\right.$��
��Rt��OCQ��Rt��OC'Q��HL����
���OQC=��OQC'��
�֡�OP��C'Q��
�ߡ�POQ=��OQC'��
���POQ=��PQO��
��PO=PQ��
��BP=QP��
��BP=OP=x��
��Rt��OPC��x2=��8-x��2+62��
��ã�x=$\frac{25}{4}$��
��S��OPQ=$\frac{1}{2}$��CO��PQ=$\frac{1}{2}$��6��$\frac{25}{4}$=$\frac{75}{4}$��
���� ������Ҫ�����˾��ε��ж��������Լ�ȫ�������ε��ж������ʡ����ɶ����������������֪ʶ����ȷ�ó�PO=PQ�ǽ���ؼ���

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д���$\frac{x+y}{xy}=\frac{2x+y}{2xy}$��$\frac{b}{a}=\frac{b+3}{a+3}$��$\frac{ab}{a+b}=\frac{-ab}{-a+b}$��$\frac{n}{m}=\frac{{n}^{2}}{{m}^{2}}$��
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
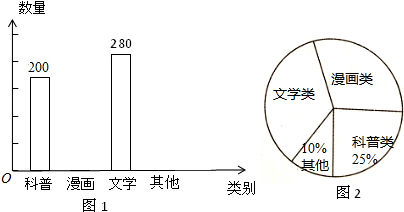
| A�� | һ���ڸ�Уѧ�����ĸ���ͼ��һ����800�� | |
| B�� | ��Уѧ��ϲ���Ķ���ѧ��ͼ���Լռ35% | |
| C�� | һ���ڸ�Уѧ������������ͼ��Լ240�� | |
| D�� | ����ѧУ�ƻ������������鹲1000�������ܸ���ѧ����Ҫȷ������ͼ���������ֻ��������� |
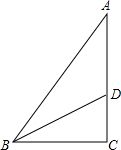 ��ֱ��������ABC�У�BC=6��AC=8����D���߶�AC�ϴ�C��A�˶�������CD=x����ABD�����Ϊy��
��ֱ��������ABC�У�BC=6��AC=8����D���߶�AC�ϴ�C��A�˶�������CD=x����ABD�����Ϊy��