题目内容
14.下列分式从左到右的变形,错误的有( )①$\frac{x+y}{xy}=\frac{2x+y}{2xy}$②$\frac{b}{a}=\frac{b+3}{a+3}$③$\frac{ab}{a+b}=\frac{-ab}{-a+b}$④$\frac{n}{m}=\frac{{n}^{2}}{{m}^{2}}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据分式的基本性质对各个选项进行判断.
解答 解:①$\frac{x+y}{xy}=\frac{2x+y}{2xy}$,分子中的y没有乘2,变形错误;
②$\frac{b}{a}=\frac{b+3}{a+3}$,不符合分式的基本性质,变形错误;
③$\frac{ab}{a+b}=\frac{-ab}{-a+b}$,分母中的b没有乘-1,变形错误;
④$\frac{n}{m}=\frac{{n}^{2}}{{m}^{2}}$,分子分母不是乘的同一个整式,变形错误.
四个都是错误的.
故选:D.
点评 此题考查分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
4.当a=-$\frac{1}{2}$时,代数式1-a2的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1$\frac{1}{4}$ | D. | -2$\frac{1}{4}$ |
5.下面的计算正确的是( )
| A. | 6b-5b=1 | B. | a+2a2=3a3 | C. | -(d-b)=b-d | D. | 2(a+c)=2a+c |
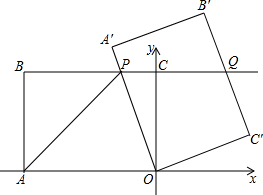 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′,此时边OA′与边BC交于点P,边B′C′与BC的延长线交于点Q,连接AP.
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′,此时边OA′与边BC交于点P,边B′C′与BC的延长线交于点Q,连接AP.