在直角三角形ABC中.BC=6.AC=8.点D在线段AC上从C向A运动．若设CD=x.△ABD的面积为y．(1)请写出y与x的关系式,(2)当△ABD的面积是△ABC的面积的$\frac{1}{3}$时.求AD．题目和参考答案——青夏教育精英家教网—

题目内容

17．

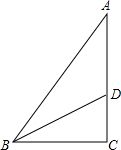在直角三角形ABC中，BC=6，AC=8，点D在线段AC上从C向A运动．若设CD=x，△ABD的面积为y．
（1）请写出y与x的关系式；
（2）当△ABD的面积是△ABC的面积的$\frac{1}{3}$时，求AD．

分析（1））△ABD的面积=$\frac{1}{2}$AD×BC，把相关数值代入化简即可；
（2）根据三角形的面积代入数值进行解答即可．

解答解：（1）=$\frac{1}{2}$×（8-x）×6=24-3x
（2）∵${S_{△ABC}}=\frac{1}{2}×6×8=24$
∴当$y=\frac{1}{3}{S_{△ABC}}=\frac{1}{3}×24=8$时，$24-3x=8，x=\frac{16}{3}$．
∴$AD=AC-CD=8-\frac{16}{3}=\frac{8}{3}$．

点评此题考查三角形面积问题，判断出所求三角形的底边及底边上的高是解决本题的突破点．

练习册系列答案

7．分解因式：x²-4y²-9z²-12yz．

5．

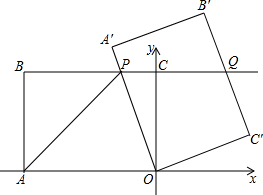如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（-8，0），直线BC经过点B（-8，6），C（0，6），将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′，此时边OA′与边BC交于点P，边B′C′与BC的延长线交于点Q，连接AP．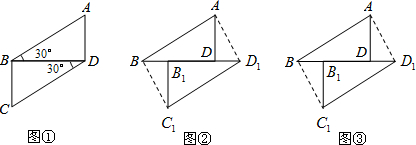
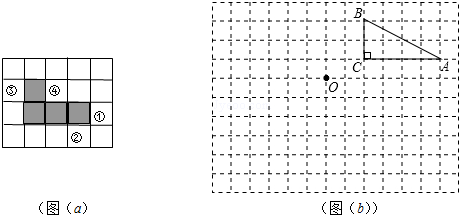
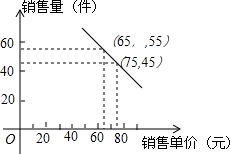（1）四边形OABC的形状是矩形．
（2）在旋转过程中，当∠PAO=∠POA，求P点坐标．
（3）在旋转过程中，当P为线段BQ中点时，连接OQ，求△OPQ的面积．

12．将两块全等的含30°角的三角尺如图①摆放在一起，设较短的直角边长为3．
（1）四边形ABCD是平行四边形吗？说出你的结论和理由．
（2）如图②，将Rt△BCD沿射线BD方向平移到Rt△B₁C₁D₁的位置，四边形ABC₁D₁是平行四边形吗？说出你的结论和理由．
（3）在Rt△BCD沿射线BD方向平移的过程中，当点B的移动距离为多少时四边形ABC₁D₁为矩形？

2．（1）如图（a），在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与与图中阴影部分构成中心对称图形，涂黑的小正方形的序号是②．
（2）如图（b），在边长为1个单位长度的小正方形组成的网格中，点A、B、C都是格点．将△ABC向左平移6个单位，作出它的像△A₁B₁C₁；
（3）如图（b），求作一个△A₂B₂C₂，并画出△A₂B₂C₂，使它与△A₁B₁C₁关于点O成中心对称．

9．

超市市场部整理出销售某品牌新款童装的销售量与销售单价的相关信息如下：
已知该童装的进价为每件60元，设销售单价为x元，销售单价不低于进价，且获利不得高于45%，设销售该款童装的利润为W元．
（1）求利润W与销售单价x之间的关系式，并求销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？
（2）若超市销售该款童装获得的利润不低于500元，试确定销售单价x的范围．

6．

如图，△ABC面积为1，第一次操作：分别延长AB，BC，CA至点A₁，B₁，C₁，使A₁B=AB，C₁B=CB，C₁A=CA，顺次连接A₁，B₁，C₁，得到△A₁B₁C₁．第二次操作：分别延长A₁B₁，B₁C₁，C₁A₁至点A₂，B₂，C₂，使A₂B₁=A₁B₁，B₂C₁=B₁C₁，C₂A₁=C₁A₁，顺次连接A₂，B₂，C₂，得到△A₂B₂C₂，…按此规律，要使得到的三角形的面积超过2014，最少经过（　　）次操作．

7．3^9m•27^m=3⁶，则m=$\frac{1}{2}$．

试题分类