题目内容
12.分解因式:(1)a4+3a2;
(2)5(a-2)3-3(2-a)2;
(3)(x-2)2-x+2;
(4)a(a-b-c)+b(b+c-a);
(5)(a-b)2(a+b)3-(b-a)3(b+a)2;
(6)-2xy+6x2y2-8x2y.
分析 (1)根据提公因式法,提取a2,可得答案;
(2)根据互为相反数的平方相等,可得公因式,根据提取公因式,可得答案;
(3)根据提公因式法,可得答案;
(4)根据只有符号不同的两个数互为相反数,可得公因式,根据提取公因式,可得答案;
(5)根据只有符号不同的两个数互为相反数,可得公因式,根据提取公因式,可得答案;
(6)根据提公因式法,可得答案.
解答 解:(1)a4+3a2=a2(a2+3);
(2)5(a-2)3-3(2-a)2=(a-2)2[5(a-2)-3]=(a-2)2(5a-13);
(3)(x-2)2-x+2=(x-2)(x-2-1)=(x-2)(x-3);
(4)a(a-b-c)+b(b+c-a)=(a-b-c)(a-b);
(5)(a-b)2(a+b)3-(b-a)3(b+a)2=(b-a)2(a+b)3-(b-a)3(b+a)2
=(b-a)2(b+a)2[(a+b)-(b-a)]
=2a(b-a)2(b+a)2;
(6)-2xy+6x2y2-8x2y=-2xy(1-3xy+4x).
点评 本题考查了因式分解,利用了提公因式法,公式法分解因式,利用相反数的乘方得出公因式是解题关键,分解要彻底.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
3.为了了解大江东产业集聚区2014年数学学业考试各分数段成绩分布情况,从中抽取 1500名考生的学业考试数学成绩进行统计分析.在这个问题中,样本容量是指( )
| A. | 1500 | |
| B. | 被抽取的1500名考生的学业考试数学成绩 | |
| C. | 被抽取的1500名考生 | |
| D. | 大江东产业集聚区2014年学业考试数学成绩 |
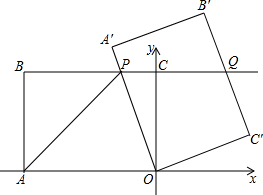 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′,此时边OA′与边BC交于点P,边B′C′与BC的延长线交于点Q,连接AP.
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′,此时边OA′与边BC交于点P,边B′C′与BC的延长线交于点Q,连接AP.