题目内容
10．已知关于x的一元二次方程x2+2（k-3）x+k2-9=0有两个不相等的实数根．（1）求实数k的取值范围；
（2）0可能是方程的一个根吗？若是，请求出它的另一个根；若不是，请说明理由．
分析 （1）直接判断△=b2-4ac＞0，进而得出答案；
（2）将x=0代入方程求出k的值，进而解方程得出答案．
解答 解：（1）△=b2-4ac=[2（k-3）]2-4（k2-9）=-24k+72＞0，
解得：k＜3；
（2）当0是方程的根，则k2-9=0，
解得：k1=3（不合题意舍去），k2=-3，
故x2-12x=0，
解得：x1=12，x2=0，
故它的另一个根为12．
点评 此题主要考查了根的判别式以及一元二次方程的解，正确得出k的值是解题关键．
练习册系列答案
智能训练练测考系列答案
相关题目
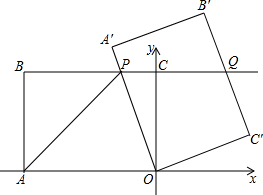如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（-8，0），直线BC经过点B（-8，6），C（0，6），将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′，此时边OA′与边BC交于点P，边B′C′与BC的延长线交于点Q，连接AP．
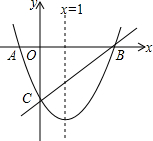如图，对称轴为直线x=1的抛物线y=ax2+bx+c交x轴于A，B，交y轴的负半轴于C，A的坐标为（-1，0），OA=$\frac{1}{3}$OC．