Question

3．△ABC≌△DEF，
（1）若△ABC的周长为32，AB=10，BC=14，则DF=8；
（2）∠A=48°，∠B=53°，则∠D=48°，∠F=79°．

Answer 1

分析 （1）首先计算出AC的长，然后根据全等三角形对应边相等可得DF=AC，进而可得答案；
（2）首先利用三角形内角和可得∠C的度数，然后根据全等三角形的对应角相等可得答案．

解答 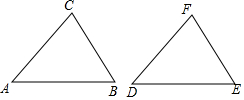解：（1）∵△ABC的周长为32，AB=10，BC=14，
∴AC=32-10-14=8，
∵△ABC≌△DEF，
∴DF=AC=8，
故答案为：8；

（2）∵∠A=48°，∠B=53°，
∴∠C=180°-48°-53°=79°，
∵△ABC≌△DEF，
∴∠D=∠A=48°，∠F=∠C=79°，
故答案为：48°；79°．

点评 此题主要考查了全等三角形的性质，以及三角形内角和定理，关键是掌握全等三角形的对应边相等；全等三角形的对应角相等．