题目内容
6.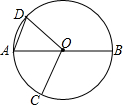 如图,AB是⊙O的直径,点C、D在⊙O上,∠BOD=∠COD,AD∥OC,则∠BOC=( )
如图,AB是⊙O的直径,点C、D在⊙O上,∠BOD=∠COD,AD∥OC,则∠BOC=( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
分析 由OA=OD可知∠OAD=∠ODA,根据三角形外角的性质得出∠OAD+∠ODA=∠BOD,即2∠OAD=∠BOD,再由平行线的性质得出∠OAD=∠AOC,故∠COD=∠AOC+∠AOD=∠OAD+∠AOD,根据∠BOD=∠COD可知∠AOD=∠OAD,故可得出∠AOD=∠OAD=60°,由此可得出∠BOD=∠COD=120°,进而可得出结论.
解答 解:∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD+∠ODA=∠BOD,即2∠OAD=∠BOD.
∵AD∥OC,
∴∠OAD=∠AOC,
∴∠COD=∠AOC+∠AOD=∠OAD+∠AOD.
∵∠BOD=∠COD,
∴∠AOD=∠OAD,
∴∠AOD=∠OAD=60°,
∴∠BOD=∠COD=120°,
∴∠BOC=360°-120°-120°=120°.
故选C.
点评 本题考查的是圆周角定理,熟知平行线的性质、三角形外角的性质等知识是解答此题的关键.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
14.把抛物线y=x2+1向右平移3个单位,再向上平移2个单位,得到抛物线( )
| A. | y=(x+3)2-1 | B. | y=(x+3)2+3 | C. | y=(x-3)2-1 | D. | y=(x-3)2+3 |
1.△ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 7 |
11.把一块长80mm、宽60mm的铁皮的4个角分别剪去一个边长相等的小正方形,做成一个底面积是1500mm2的无盖铁盒.若设小正方形的边长为x mm,下面所列的方程中,正确的是( )
| A. | (80-x)(60-x)=1500 | B. | (80-2x)(60-2x)=1500 | C. | (80-2x)(60-x)=1500 | D. | (80-x)(60-2x)=1500 |
18.下列各对数中,互为相反数的是( )
| A. | 2与$\frac{1}{2}$ | B. | -(-3)和+|-3| | C. | -(-2)与-|-2| | D. | +(-5)与-(+5) |
15.下列计算正确的是( )
| A. | 2a-a=2 | B. | m6÷m2=m3 | ||
| C. | x2010+x2010=2x2010 | D. | t2•t3=t6 |