题目内容
1.△ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是( )| A. | 8 | B. | 10 | C. | 8或10 | D. | 7 |
分析 先利用因式分解法解方程得到x1=3,x2=5,再根据三角形三边的关系可判断△ABC的第三边长为3,然后计算△ABC的周长.
解答 解:∵x2-8x+15=0,
∴(x-3)(x-5)=0,
∴x-3=0或x-5=0,
∴x1=3,x2=5,
∵2+3≠5,
∴△ABC的第三边长为3,
∴△ABC的周长为2+3+3=8.
故选A.
点评 本题考查了解一元二次方程-因式分解法:就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了三角形三边的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.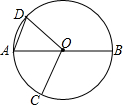 如图,AB是⊙O的直径,点C、D在⊙O上,∠BOD=∠COD,AD∥OC,则∠BOC=( )
如图,AB是⊙O的直径,点C、D在⊙O上,∠BOD=∠COD,AD∥OC,则∠BOC=( )
 如图,AB是⊙O的直径,点C、D在⊙O上,∠BOD=∠COD,AD∥OC,则∠BOC=( )
如图,AB是⊙O的直径,点C、D在⊙O上,∠BOD=∠COD,AD∥OC,则∠BOC=( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
13.下列有理数中,负数的个数是( )
①-(-1)②-(-2)2③-|-3|④-(-4)3⑤-22.
①-(-1)②-(-2)2③-|-3|④-(-4)3⑤-22.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,已知AB,CD相交于O,△ACO≌△BDO,AE=BF,求证:CE=FD.
如图,已知AB,CD相交于O,△ACO≌△BDO,AE=BF,求证:CE=FD.