��Ŀ����
14��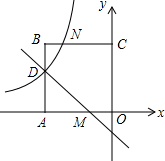 ��ͼ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O������ԭ���غϣ���C������Ϊ��0��3������A��x��ĸ������ϣ���D��M�ֱ��ڱ�AB��OA�ϣ���AD=2DB��AM=2MO��һ�κ���y=kx+b��ͼ�����D��M������������y=$\frac{m}{x}$��ͼ����D����BC�Ľ���ΪN��
��ͼ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O������ԭ���غϣ���C������Ϊ��0��3������A��x��ĸ������ϣ���D��M�ֱ��ڱ�AB��OA�ϣ���AD=2DB��AM=2MO��һ�κ���y=kx+b��ͼ�����D��M������������y=$\frac{m}{x}$��ͼ����D����BC�Ľ���ΪN����1������������һ�κ����ı���ʽ��
��2������P��ֱ��DM�ϣ���ʹ��OPM��������ı���OMNC�������ȣ����P�����꣮
���� ��1����������OABC�Ķ���C���꣬ȷ�����߳������ĸ���Ϊֱ�ǣ�����AD=2DB�����AD�ij���ȷ����D���꣬���뷴��������ʽ���m��ֵ������AM=2MO��ȷ����MO�ij�����M���꣬��M��D�������һ�κ�������ʽ���k��b��ֵ������ȷ����һ�κ�������ʽ��
��2����y=3���뷴��������ʽ���x��ֵ��ȷ����N���꣬�õ�NC�ij�����P��x��y�������ݡ�OPM��������ı���OMNC�������ȣ����y��ֵ�������õ�x��ֵ��ȷ����P���꼴�ɣ�
��� �⣺��1����������OABC�Ķ���C��0��3����
��OA=AB=BC=OC=3����OAB=��B=��BCO=90�㣬
��AD=2DB��
��AD=$\frac{2}{3}$AB=2��
��D��-3��2����
��D�������y=$\frac{m}{x}$�ã�m=-6��
�෴��������ʽΪy=-$\frac{6}{x}$��
��AM=2MO��
��MO=$\frac{1}{3}$OA=1����M��-1��0����
��M��D�������y=kx+b�еã�$\left\{\begin{array}{l}{-k+b=0}\\{-3k+b=2}\end{array}\right.$��
��ã�k=b=-1��
��ֱ��DM����ʽΪy=-x-1��
��2����y=3����y=-$\frac{6}{x}$�ã�x=-2��
��N��-2��3������NC=2��
��P��x��y����
�ߡ�OPM��������ı���OMNC�������ȣ�
��$\frac{1}{2}$��OM+NC��•OC=$\frac{1}{2}$OM|y|����|y|=9��
��ã�y=��9��
��y=9ʱ��x=-10����y=-9ʱ��x=8��
��P������-10��9����8��-9����
���� ���⿼����һ�κ����뷴���������Ľ������⣬�漰��֪ʶ�У�����ϵ����ȷ��һ�κ�������������������ʽ��������ͼ�����ʣ������ε����ʣ��Լ�������������㣬�������մ���ϵ�����ǽⱾ��Ĺؼ���

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д� ����ף�㿼�Գɹ����������ֱַ�д��һ����������������ϣ�������������չ��ͼ��ͼ��ʾ����������������У��롰�㡱����Ե����ǣ�������
����ף�㿼�Գɹ����������ֱַ�д��һ����������������ϣ�������������չ��ͼ��ͼ��ʾ����������������У��롰�㡱����Ե����ǣ�������| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
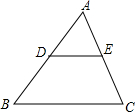 ��ͼ����D��E�ֱ�Ϊ��ABC�ı�AB��AC�ϵ��е㣬���ADE��������ı���BCED������ı�Ϊ��������
��ͼ����D��E�ֱ�Ϊ��ABC�ı�AB��AC�ϵ��е㣬���ADE��������ı���BCED������ı�Ϊ��������| A�� | 1��2 | B�� | 1��3 | C�� | 1��4 | D�� | 1��1 |
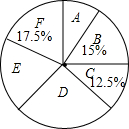 ijѧУ��Ϊ��һѧ������ABCDEF��6��ѡ�Σ���ѡȡ����ѧ�������ˡ�����ϲ����һ��ѡ�Ρ����飬�����������Ƴ���ͼͳ��ͼ������������
ijѧУ��Ϊ��һѧ������ABCDEF��6��ѡ�Σ���ѡȡ����ѧ�������ˡ�����ϲ����һ��ѡ�Ρ����飬�����������Ƴ���ͼͳ��ͼ������������| ѡ�� | A | B | C | D | E | F |
| ���� | 40 | 60 | 100 |
| A�� | ��α������ѧ������Ϊ400�� | |
| B�� | ����ͳ��ͼ��E�������ε�Բ�Ľ�Ϊ72�� | |
| C�� | �������ѧ����ϲ��ѡ��E��F�������ֱ�Ϊ80��70 | |
| D�� | ϲ��ѡ��C���������� |
 ��ͼ��l1��l2����1=56�㣬���2�Ķ���Ϊ��������
��ͼ��l1��l2����1=56�㣬���2�Ķ���Ϊ��������| A�� | 34�� | B�� | 56�� | C�� | 124�� | D�� | 146�� |
| A�� | 6 | B�� | 7 | C�� | 8 | D�� | 9 |

| A�� | 2n+1 | B�� | n2-1 | C�� | n2+2n | D�� | 5n-2 |
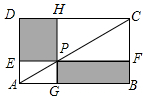 ��ͼ����P�ھ���ABCD�ĶԽ���AC�ϣ��Ҳ����A��C�غϣ�����P�ֱ�����AB��AD��ƽ���ߣ�������Ա��ڵ�E��F��G��H��
��ͼ����P�ھ���ABCD�ĶԽ���AC�ϣ��Ҳ����A��C�غϣ�����P�ֱ�����AB��AD��ƽ���ߣ�������Ա��ڵ�E��F��G��H�� �����������ɡ����ί��ƻ������˶����ַ��������ߣ�Ϊ�ˣ������˲��ֲ����ߣ��Ծ���������ɫ����ɫ����ɫ����ɫ������ɫ�˶��������������ݵõ��ĵ������ݣ����Ƴ���ͼ��ʾ������ͳ��ͼ�������λ����12000�������ߣ����������ѡ���ɫ�˶�����Լ��2400����
�����������ɡ����ί��ƻ������˶����ַ��������ߣ�Ϊ�ˣ������˲��ֲ����ߣ��Ծ���������ɫ����ɫ����ɫ����ɫ������ɫ�˶��������������ݵõ��ĵ������ݣ����Ƴ���ͼ��ʾ������ͳ��ͼ�������λ����12000�������ߣ����������ѡ���ɫ�˶�����Լ��2400����